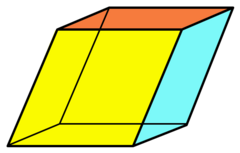
Rhombohedron

Short description: Polyhedron with six rhombi as faces

Rhombohedron
Type	prism
Faces	6 rhombi
Edges	12
Vertices	8
Symmetry group	Ci , [2+,2+], (×), order 2
Properties	convex, equilateral, zonohedron, parallelohedron

In geometry, a rhombohedron (also called a rhombic hexahedron or, inaccurately, a rhomboid) is a three-dimensional figure with six faces which are rhombi. It is a special case of a parallelepiped where all edges are the same length. It can be used to define the rhombohedral lattice system, a honeycomb with rhombohedral cells. A cube is a special case of a rhombohedron with all sides square.

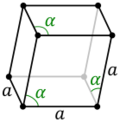
In general a rhombohedron can have up to three types of rhombic faces in congruent opposite pairs, C_i symmetry, order 2.

Four points forming non-adjacent vertices of a rhombohedron necessarily form the four vertices of an orthocentric tetrahedron, and all orthocentric tetrahedra can be formed in this way.

Rhombohedral lattice system

The rhombohedral lattice system has rhombohedral cells, with 6 congruent rhombic faces forming a trigonal trapezohedron:

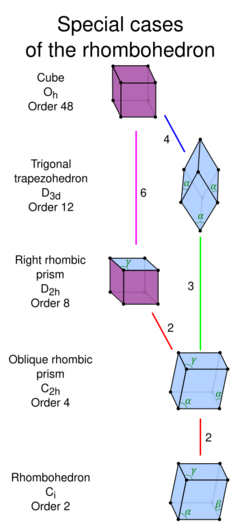
Special cases by symmetry

Special cases of the rhombohedron

Form	Cube	Trigonal trapezohedron	Right rhombic prism	Oblique rhombic prism
Angle constraints	[math]\displaystyle{ \alpha=\beta=\gamma=90^\circ }[/math]	[math]\displaystyle{ \alpha=\beta=\gamma }[/math]	[math]\displaystyle{ \alpha=\beta=90^\circ }[/math]	[math]\displaystyle{ \alpha=\beta }[/math]
Symmetry	Oh order 48	D3d order 12	D2h order 8	C2h order 4
Faces	6 squares	6 congruent rhombi	2 rhombi, 4 squares	6 rhombi

• Cube: with O_h symmetry, order 48. All faces are squares.
• Trigonal trapezohedron (also called isohedral rhombohedron): with D_3d symmetry, order 12. All non-obtuse internal angles of the faces are equal (all faces are congruent rhombi). This can be seen by stretching a cube on its body-diagonal axis. For example, a regular octahedron with two regular tetrahedra attached on opposite faces constructs a 60 degree trigonal trapezohedron.
• Right rhombic prism: with D_2h symmetry, order 8. It is constructed by two rhombi and four squares. This can be seen by stretching a cube on its face-diagonal axis. For example, two right prisms with regular triangular bases attached together makes a 60 degree right rhombic prism.
• Oblique rhombic prism: with C_2h symmetry, order 4. It has only one plane of symmetry, through four vertices, and six rhombic faces.

Solid geometry

For a unit (i.e.: with side length 1) isohedral rhombohedron, with rhombic acute angle [math]\displaystyle{ \theta~ }[/math], with one vertex at the origin (0, 0, 0), and with one edge lying along the x-axis, the three generating vectors are

e₁ : [math]\displaystyle{ \biggl(1, 0, 0\biggr), }[/math]

e₂ : [math]\displaystyle{ \biggl(\cos\theta, \sin\theta, 0\biggr), }[/math]

e₃ : [math]\displaystyle{ \biggl(\cos\theta, {\cos\theta-\cos^2\theta\over \sin\theta}, {\sqrt{1-3\cos^2\theta+2\cos^3\theta} \over \sin\theta} \biggr). }[/math]

The other coordinates can be obtained from vector addition of the 3 direction vectors: e₁ + e₂ , e₁ + e₃ , e₂ + e₃ , and e₁ + e₂ + e₃ .

The volume [math]\displaystyle{ V }[/math] of an isohedral rhombohedron, in terms of its side length [math]\displaystyle{ a }[/math] and its rhombic acute angle [math]\displaystyle{ \theta~ }[/math], is a simplification of the volume of a parallelepiped, and is given by

[math]\displaystyle{ V = a^3(1-\cos\theta)\sqrt{1+2\cos\theta} = a^3\sqrt{(1-\cos\theta)^2(1+2\cos\theta)} = a^3\sqrt{1-3\cos^2\theta+2\cos^3\theta}~. }[/math]

We can express the volume [math]\displaystyle{ V }[/math] another way :

[math]\displaystyle{ V = 2\sqrt{3} ~ a^3 \sin^2\left(\frac{\theta}{2}\right) \sqrt{1-\frac{4}{3}\sin^2\left(\frac{\theta}{2}\right)}~. }[/math]

As the area of the (rhombic) base is given by [math]\displaystyle{ a^2\sin\theta~ }[/math], and as the height of a rhombohedron is given by its volume divided by the area of its base, the height [math]\displaystyle{ h }[/math] of an isohedral rhombohedron in terms of its side length [math]\displaystyle{ a }[/math] and its rhombic acute angle [math]\displaystyle{ \theta }[/math] is given by

[math]\displaystyle{ h = a~{(1-\cos\theta)\sqrt{1+2\cos\theta} \over \sin\theta} = a~{\sqrt{1-3\cos^2\theta+2\cos^3\theta} \over \sin\theta}~. }[/math]

Note:

[math]\displaystyle{ h = a~z }[/math]₃ , where [math]\displaystyle{ z }[/math]₃ is the third coordinate of e₃ .

The body diagonal between the acute-angled vertices is the longest. By rotational symmetry about that diagonal, the other three body diagonals, between the three pairs of opposite obtuse-angled vertices, are all the same length.

See also

• Lists of shapes

External links

• Weisstein, Eric W.. "Rhombohedron". http://mathworld.wolfram.com/Rhombohedron.html. 
• Volume Calculator https://rechneronline.de/pi/rhombohedron.php