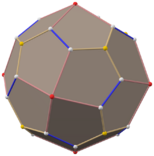
Catalan solid
In mathematics, a Catalan solid, or Archimedean dual, is a polyhedron that is dual to an Archimedean solid. There are 13 Catalan solids. They are named for the Belgian mathematician Eugène Catalan, who first described them in 1865.
The Catalan solids are all convex. They are face-transitive but not vertex-transitive. This is because the dual Archimedean solids are vertex-transitive and not face-transitive. Note that unlike Platonic solids and Archimedean solids, the faces of Catalan solids are not regular polygons. However, the vertex figures of Catalan solids are regular, and they have constant dihedral angles. Being face-transitive, Catalan solids are isohedra.
Additionally, two of the Catalan solids are edge-transitive: the rhombic dodecahedron and the rhombic triacontahedron. These are the duals of the two quasi-regular Archimedean solids.
Just as prisms and antiprisms are generally not considered Archimedean solids, bipyramids and trapezohedra are generally not considered Catalan solids, despite being face-transitive.
Two of the Catalan solids are chiral: the pentagonal icositetrahedron and the pentagonal hexecontahedron, dual to the chiral snub cube and snub dodecahedron. These each come in two enantiomorphs. Not counting the enantiomorphs, bipyramids, and trapezohedra, there are a total of 13 Catalan solids.
List of Catalan solids and their duals
| Conway name | Archimedean dual | Face polygon |
Orthogonal wireframes |
Pictures | Face angles (°) | Dihedral angle (°) | Midradius[1] | Faces | Edges | Vert | Sym. |
|---|---|---|---|---|---|---|---|---|---|---|---|
| triakis tetrahedron "kT" |
truncated tetrahedron | Isosceles V3.6.6 |
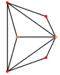 60px 60px
|
 
|
112.885 33.557 33.557 |
129.521 | 1.0607 | 12 | 18 | 8 | Td |
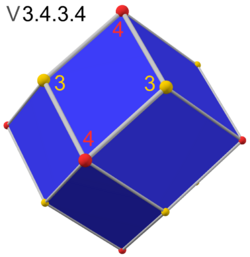
| rhombic dodecahedron "jC" |
cuboctahedron | Rhombus V3.4.3.4 |
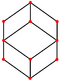 60px 60px
|
 
|
70.529 109.471 70.529 109.471 |
120 | 0.8660 | 12 | 24 | 14 | Oh |
| triakis octahedron "kO" |
truncated cube | Isosceles V3.8.8 |
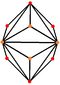 60px 60px
|
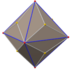 
|
117.201 31.400 31.400 |
147.350 | 1.7071 | 24 | 36 | 14 | Oh |
| tetrakis hexahedron "kC" |
truncated octahedron | Isosceles V4.6.6 |
 60px 60px
|
 
|
83.621 48.190 48.190 |
143.130 | 1.5000 | 24 | 36 | 14 | Oh |
| deltoidal icositetrahedron "oC" |
rhombicuboctahedron | Kite V3.4.4.4 |
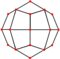 60px 60px
|
 
|
81.579 81.579 81.579 115.263 |
138.118 | 1.3066 | 24 | 48 | 26 | Oh |
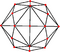
| disdyakis dodecahedron "mC" |
truncated cuboctahedron | Scalene V4.6.8 |
 60px 60px
|
 
|
87.202 55.025 37.773 |
155.082 | 2.2630 | 48 | 72 | 26 | Oh |
| pentagonal icositetrahedron "gC" |
snub cube | Pentagon V3.3.3.3.4 |
 60px 60px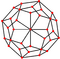
|
 
|
114.812 114.812 114.812 114.812 80.752 |
136.309 | 1.2472 | 24 | 60 | 38 | O |
| rhombic triacontahedron "jD" |
icosidodecahedron | Rhombus V3.5.3.5 |
 60px 60px
|
 
|
63.435 116.565 63.435 116.565 |
144 | 1.5388 | 30 | 60 | 32 | Ih |
| triakis icosahedron "kI" |
truncated dodecahedron | Isosceles V3.10.10 |
 60px 60px
|
 
|
119.039 30.480 30.480 |
160.613 | 2.9271 | 60 | 90 | 32 | Ih |
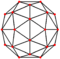
| pentakis dodecahedron "kD" |
truncated icosahedron | Isosceles V5.6.6 |
 60px 60px
|
 
|
68.619 55.691 55.691 |
156.719 | 2.4271 | 60 | 90 | 32 | Ih |
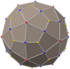
| deltoidal hexecontahedron "oD" |
rhombicosidodecahedron | Kite V3.4.5.4 |
 60px 60px
|
|
86.974 67.783 86.974 118.269 |
154.121 | 2.1763 | 60 | 120 | 62 | Ih |
| disdyakis triacontahedron "mD" |
truncated icosidodecahedron | Scalene V4.6.10 |
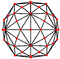 60px 60px
|
 
|
88.992 58.238 32.770 |
164.888 | 3.7694 | 120 | 180 | 62 | Ih |
| pentagonal hexecontahedron "gD" |
snub dodecahedron | Pentagon V3.3.3.3.5 |
 60px 60px
|
 
|
118.137 118.137 118.137 118.137 67.454 |
153.179 | 2.0971 | 60 | 150 | 92 | I |
| ordered by size |
|---|
|
The Catalan solids' Archimedean duals, all shown with the same edge length. Sorted by midradius in descending order: Error creating thumbnail: Unable to save thumbnail to destination
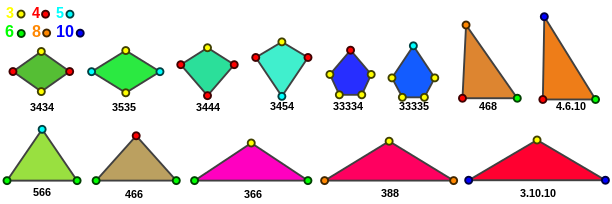
All faces of Catalan solids, same scale as above: |
Symmetry
The Catalan solids, along with their dual Archimedean solids, can be grouped in those with tetrahedral, octahedral and icosahedral symmetry. For both octahedral and icosahedral symmetry there are six forms. The only Catalan solid with genuine tetrahedral symmetry is the triakis tetrahedron (dual of the truncated tetrahedron). The rhombic dodecahedron and tetrakis hexahedron have octahedral symmetry, but they can be colored to have only tetrahedral symmetry. Rectification and snub also exist with tetrahedral symmetry, but they are Platonic instead of Archimedean, so their duals are Platonic instead of Catalan. (They are shown with brown background in the table below.)
| Archimedean (Platonic) |

|

|

|

|
Error creating thumbnail: File with dimensions greater than 12.5 MP
|

|
|---|---|---|---|---|---|---|
| Catalan (Platonic) |

|

|

|

|

|

|
| Archimedean | 
|

|

|

|

|

|
|---|---|---|---|---|---|---|
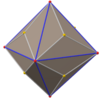
| Catalan | 
|
|

|

|

|

|
| Archimedean | 
|

|

|

|

|

|
|---|---|---|---|---|---|---|
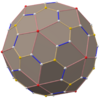
| Catalan | 
|

|

|

|

|
|
Geometry
All dihedral angles of a Catalan solid are equal. Denoting their value by [math]\displaystyle{ \theta }[/math] , and denoting the face angle at the vertices where [math]\displaystyle{ p }[/math] faces meet by [math]\displaystyle{ \alpha_p }[/math], we have
- [math]\displaystyle{ \sin(\theta/2)=\cos(\pi/p)/\cos(\alpha_p/2) }[/math].
This can be used to compute [math]\displaystyle{ \theta }[/math] and [math]\displaystyle{ \alpha_p }[/math], [math]\displaystyle{ \alpha_q }[/math], ... , from [math]\displaystyle{ p }[/math], [math]\displaystyle{ q }[/math] ... only.
Triangular faces
Of the 13 Catalan solids, 7 have triangular faces. These are of the form Vp.q.r, where p, q and r take their values among 3, 4, 5, 6, 8 and 10. The angles [math]\displaystyle{ \alpha_p }[/math], [math]\displaystyle{ \alpha_q }[/math] and [math]\displaystyle{ \alpha_r }[/math] can be computed in the following way. Put [math]\displaystyle{ a = 4\cos^2(\pi/p) }[/math], [math]\displaystyle{ b = 4\cos^2(\pi/q) }[/math], [math]\displaystyle{ c = 4\cos^2(\pi/r) }[/math] and put
- [math]\displaystyle{ S = -a^2-b^2-c^2+2 a b + 2 b c + 2 c a }[/math].
Then
- [math]\displaystyle{ \cos(\alpha_p) = \frac{S}{2 b c} - 1 }[/math],
- [math]\displaystyle{ \sin(\alpha_p/2) = \frac{-a+b+c}{2\sqrt{b c}} }[/math].
For [math]\displaystyle{ \alpha_q }[/math] and [math]\displaystyle{ \alpha_r }[/math] the expressions are similar of course. The dihedral angle [math]\displaystyle{ \theta }[/math] can be computed from
- [math]\displaystyle{ \cos(\theta)=1- 2 a b c/S }[/math].
Applying this, for example, to the disdyakis triacontahedron ([math]\displaystyle{ p=4 }[/math], [math]\displaystyle{ q=6 }[/math] and [math]\displaystyle{ r=10 }[/math], hence [math]\displaystyle{ a = 2 }[/math], [math]\displaystyle{ b = 3 }[/math] and [math]\displaystyle{ c = \phi + 2 }[/math], where [math]\displaystyle{ \phi }[/math] is the golden ratio) gives [math]\displaystyle{ \cos(\alpha_4)=\frac{2-\phi}{6(2+\phi)}= \frac{7-4\phi}{30} }[/math] and [math]\displaystyle{ \cos(\theta) = \frac{-10-7\phi}{14+5\phi}=\frac{-48\phi-155}{241} }[/math].
Quadrilateral faces
Of the 13 Catalan solids, 4 have quadrilateral faces. These are of the form Vp.q.p.r, where p, q and r take their values among 3, 4, and 5. The angle [math]\displaystyle{ \alpha_p }[/math]can be computed by the following formula:
- [math]\displaystyle{ \cos(\alpha_p)= \frac{2\cos^2(\pi/p)-\cos^2(\pi/q)-\cos^2(\pi/r)}{2\cos^2(\pi/p)+2\cos(\pi/q)\cos(\pi/r)} }[/math].
From this, [math]\displaystyle{ \alpha_q }[/math], [math]\displaystyle{ \alpha_r }[/math] and the dihedral angle can be easily computed. Alternatively, put [math]\displaystyle{ a = 4\cos^2(\pi/p) }[/math], [math]\displaystyle{ b = 4\cos^2(\pi/q) }[/math], [math]\displaystyle{ c = 4\cos^2(\pi/p)+4\cos(\pi/q)\cos(\pi/r) }[/math]. Then [math]\displaystyle{ \alpha_p }[/math] and [math]\displaystyle{ \alpha_q }[/math] can be found by applying the formulas for the triangular case. The angle [math]\displaystyle{ \alpha_r }[/math] can be computed similarly of course. The faces are kites, or, if [math]\displaystyle{ q=r }[/math], rhombi. Applying this, for example, to the deltoidal icositetrahedron ([math]\displaystyle{ p=4 }[/math], [math]\displaystyle{ q=3 }[/math] and [math]\displaystyle{ r=4 }[/math]), we get [math]\displaystyle{ \cos(\alpha_4)=\frac{1}{2}-\frac{1}{4}\sqrt{2} }[/math].
Pentagonal faces
Of the 13 Catalan solids, 2 have pentagonal faces. These are of the form Vp.p.p.p.q, where p=3, and q=4 or 5. The angle [math]\displaystyle{ \alpha_p }[/math]can be computed by solving a degree three equation:
- [math]\displaystyle{ 8\cos^2(\pi/p)\cos^3(\alpha_p)-8\cos^2(\pi/p)\cos^2(\alpha_p)+\cos^2(\pi/q)=0 }[/math].
Metric properties
For a Catalan solid [math]\displaystyle{ \bf C }[/math] let [math]\displaystyle{ \bf A }[/math] be the dual with respect to the midsphere of [math]\displaystyle{ \bf C }[/math]. Then [math]\displaystyle{ \bf A }[/math] is an Archimedean solid with the same midsphere. Denote the length of the edges of [math]\displaystyle{ \bf A }[/math] by [math]\displaystyle{ l }[/math]. Let [math]\displaystyle{ r }[/math] be the inradius of the faces of [math]\displaystyle{ \bf C }[/math], [math]\displaystyle{ r_m }[/math] the midradius of [math]\displaystyle{ \bf C }[/math] and [math]\displaystyle{ \bf A }[/math], [math]\displaystyle{ r_i }[/math] the inradius of [math]\displaystyle{ \bf C }[/math], and [math]\displaystyle{ r_c }[/math] the circumradius of [math]\displaystyle{ \bf A }[/math]. Then these quantities can be expressed in [math]\displaystyle{ l }[/math] and the dihedral angle [math]\displaystyle{ \theta }[/math] as follows:
- [math]\displaystyle{ r^2=\frac{l^2}{8}(1-\cos\theta) }[/math],
- [math]\displaystyle{ r_m^2=\frac{l^2}{4}\frac{1-\cos\theta}{1+\cos\theta} }[/math],
- [math]\displaystyle{ r_i^2=\frac{l^2}{8}\frac{(1-\cos\theta)^2}{1+\cos\theta} }[/math],
- [math]\displaystyle{ r_c^2=\frac{l^2}{2}\frac{1}{1+\cos\theta} }[/math].
These quantities are related by [math]\displaystyle{ r_m^2=r_i^2+r^2 }[/math], [math]\displaystyle{ r_c^2=r_m^2+l^2/4 }[/math] and [math]\displaystyle{ r_i r_c=r_m^2 }[/math].
As an example, let [math]\displaystyle{ \bf A }[/math] be a cuboctahedron with edge length [math]\displaystyle{ l=1 }[/math]. Then [math]\displaystyle{ \bf C }[/math] is a rhombic dodecahedron. Applying the formula for quadrilateral faces with [math]\displaystyle{ p=4 }[/math] and [math]\displaystyle{ q=r=3 }[/math] gives [math]\displaystyle{ \cos \theta=-1/2 }[/math], hence [math]\displaystyle{ r_i=3/4 }[/math], [math]\displaystyle{ r_m=\frac{1}{2}\sqrt{3} }[/math], [math]\displaystyle{ r_c=1 }[/math], [math]\displaystyle{ r=\frac{1}{4}\sqrt{3} }[/math].
All vertices of [math]\displaystyle{ \bf C }[/math] of type [math]\displaystyle{ p }[/math] lie on a sphere with radius [math]\displaystyle{ r_{c,p} }[/math] given by
- [math]\displaystyle{ r_{c,p}^2=r_i^2+\frac{2r^2}{1-\cos\alpha_p} }[/math],
and similarly for [math]\displaystyle{ q,r,\ldots }[/math].
Dually, there is a sphere which touches all faces of [math]\displaystyle{ \bf A }[/math] which are regular [math]\displaystyle{ p }[/math]-gons (and similarly for [math]\displaystyle{ q,r,\ldots }[/math]) in their center. The radius [math]\displaystyle{ r_{i,p} }[/math] of this sphere is given by
- [math]\displaystyle{ r_{i,p}^2=r_m^2-\frac{l^2}{4}\cot^2(\pi/p) }[/math].
These two radii are related by [math]\displaystyle{ r_{i,p}r_{c,p}=r_m^2 }[/math]. Continuing the above example: [math]\displaystyle{ \cos\alpha_3=-1/3 }[/math] and [math]\displaystyle{ \cos\alpha_4=1/3 }[/math], which gives [math]\displaystyle{ r_{c,3}=\frac{3}{8}\sqrt{6} }[/math], [math]\displaystyle{ r_{c,4}=\frac{3}{4}\sqrt{2} }[/math], [math]\displaystyle{ r_{i,3}=\frac{1}{3}\sqrt{6} }[/math] and [math]\displaystyle{ r_{i,4}=\frac{1}{2}\sqrt{2} }[/math].
If [math]\displaystyle{ P }[/math] is a vertex of [math]\displaystyle{ \bf C }[/math] of type [math]\displaystyle{ p }[/math], [math]\displaystyle{ e }[/math] an edge of [math]\displaystyle{ \bf C }[/math] starting at [math]\displaystyle{ P }[/math], and [math]\displaystyle{ P^\prime }[/math] the point where the edge [math]\displaystyle{ e }[/math] touches the midsphere of [math]\displaystyle{ \bf C }[/math], denote the distance [math]\displaystyle{ P P^\prime }[/math] by [math]\displaystyle{ l_p }[/math]. Then the edges of [math]\displaystyle{ \bf C }[/math] joining vertices of type [math]\displaystyle{ p }[/math] and type [math]\displaystyle{ q }[/math] have length [math]\displaystyle{ l_{p, q} = l_p + l_q }[/math]. These quantities can be computed by
- [math]\displaystyle{ l_p=\frac{l}{2}\frac{\cos(\pi/p)}{\sin(\alpha_p/2)} }[/math],
and similarly for [math]\displaystyle{ q, r, \ldots }[/math]. Continuing the above example: [math]\displaystyle{ \sin(\alpha_3/2)=\frac{1}{3}\sqrt{6} }[/math], [math]\displaystyle{ \sin(\alpha_4/2)=\frac{1}{3}\sqrt{3} }[/math], [math]\displaystyle{ l_3=\frac{1}{8}\sqrt{6} }[/math], [math]\displaystyle{ l_4=\frac{1}{4}\sqrt{6} }[/math], so the edges of the rhombic dodecahedron have length [math]\displaystyle{ l_{3,4}=\frac{3}{8}\sqrt{6} }[/math].
The dihedral angles [math]\displaystyle{ \alpha_{p, q} }[/math]between [math]\displaystyle{ p }[/math]-gonal and [math]\displaystyle{ q }[/math]-gonal faces of [math]\displaystyle{ \bf A }[/math] satisfy
- [math]\displaystyle{ \cos \alpha_{p,q} = \frac{l^2}{4}\frac{\cot(\pi/p)\cot(\pi/q)}{r_m^2}-\frac{r_{i, p}r_{i, q}}{r_m^2} = \frac{l_p l_q-r_m^2}{r_{c,p}r_{c,q}} }[/math].
Finishing the rhombic dodecahedron example, the dihedral angle [math]\displaystyle{ \alpha_{3,4} }[/math] of the cuboctahedron is given by [math]\displaystyle{ \cos \alpha_{3,4}=-\frac{1}{3}\sqrt{3} }[/math].
Construction
The face of any Catalan polyhedron may be obtained from the vertex figure of the dual Archimedean solid using the Dorman Luke construction.[2]
Application to other solids
All of the formulae of this section apply to the Platonic solids, and bipyramids and trapezohedra with equal dihedral angles as well, because they can be derived from the constant dihedral angle property only. For the pentagonal trapezohedron, for example, with faces V3.3.5.3, we get [math]\displaystyle{ \cos(\alpha_3)=\frac{1}{4}-\frac{1}{4}\sqrt{5} }[/math], or [math]\displaystyle{ \alpha_3=108^{\circ} }[/math]. This is not surprising: it is possible to cut off both apexes in such a way as to obtain a regular dodecahedron.
See also
- List of uniform tilings Shows dual uniform polygonal tilings similar to the Catalan solids
- Conway polyhedron notation A notational construction process
- Archimedean solid
- Johnson solid
Notes
- ↑ Weisstein, Eric W.. "Archimedean Solid" (in en). https://mathworld.wolfram.com/.
- ↑ (Cundy Rollett), p. 117; (Wenninger 1983), p. 30.
References
- Eugène Catalan Mémoire sur la Théorie des Polyèdres. J. l'École Polytechnique (Paris) 41, 1-71, 1865.
- Mathematical Models (2nd ed.), Oxford: Clarendon Press, 1961.
- Gailiunas, P.; Sharp, J. (2005), "Duality of polyhedra", International Journal of Mathematical Education in Science and Technology 36 (6): 617–642, doi:10.1080/00207390500064049.
- Alan Holden Shapes, Space, and Symmetry. New York: Dover, 1991.
- Wenninger, Magnus (1983), Dual Models, Cambridge University Press, ISBN 978-0-521-54325-5 (The thirteen semiregular convex polyhedra and their duals)
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (Section 3-9)
- Anthony Pugh (1976). Polyhedra: A visual approach. California: University of California Press Berkeley. ISBN 0-520-03056-7. Chapter 4: Duals of the Archimedean polyhedra, prisma and antiprisms
External links
- Weisstein, Eric W.. "Catalan Solids". http://mathworld.wolfram.com/CatalanSolid.html.
- Weisstein, Eric W.. "Isohedron". http://mathworld.wolfram.com/Isohedron.html.
- Catalan Solids – at Visual Polyhedra
- Archimedean duals – at Virtual Reality Polyhedra
- Interactive Catalan Solid in Java
- Download link for Catalan's original 1865 publication – with beautiful figures, PDF format
 |