Innovation Method
In statistics, the Innovation Method provides an estimator for the parameters of stochastic differential equations given a time series of (potentially noisy) observations of the state variables. In the framework of continuous-discrete state space models, the innovation estimator is obtained by maximizing the log-likelihood of the corresponding discrete-time innovation process with respect to the parameters. The innovation estimator can be classified as a M-estimator, a quasi-maximum likelihood estimator or a prediction error estimator depending on the inferential considerations that want to be emphasized. The innovation method is a system identification technique for developing mathematical models of dynamical systems from measured data and for the optimal design of experiments.
Background
Stochastic differential equations (SDEs) have become an important mathematical tool for describing the time evolution of several random phenomenon in natural, social and applied sciences. Statistical inference for SDEs is thus of great importance in applications for model building, model selection, model identification and forecasting. To carry out statistical inference for SDEs, measurements of the state variables of these random phenomena are indispensable. Usually, in practice, only a few state variables are measured by physical devices that introduce random measurement errors (observational errors).
Mathematical model for inference
The innovation estimator.[1] for SDEs is defined in the framework of continuous-discrete state space models.[2] These models arise as natural mathematical representation of the temporal evolution of continuous random phenomena and their measurements in a succession of time instants. In the simplest formulation, these continuous-discrete models [2] are expressed in term of a SDE of the form
[math]\displaystyle{ \qquad\qquad d\mathbf{x}(t) = \mathbf{f} ( t,\mathbf{x}(t);\theta) dt +\sum_{i=1}^m \mathbf{g}_{i}\ (t, \mathbf{x}(t);\theta)\ d\mathbf{w}^{i}(t) \qquad \qquad (1) }[/math]
describing the time evolution of [math]\displaystyle{ d }[/math] state variables [math]\displaystyle{ \mathbf{x} }[/math] of the phenomenon for all time instant [math]\displaystyle{ t \ge t_0 }[/math], and an observation equation
[math]\displaystyle{ \qquad\qquad \mathbf{z}_{t_k} = \mathbf{Cx}(t_k)+\mathbf{e}_{t_k} \qquad\qquad (2) }[/math]
describing the time series of measurements [math]\displaystyle{ \mathbf{z}_{t_0},...,\mathbf{z}_{t_{M-1}} }[/math]of at least one of the variables [math]\displaystyle{ \mathbf{x} }[/math] of the random phenomenon on [math]\displaystyle{ M }[/math] time instants [math]\displaystyle{ t_0 \ ,..., \ t_{M-1} }[/math]. In the model (1)-(2), [math]\displaystyle{ \mathbf{f} }[/math] and [math]\displaystyle{ \mathbf{g}_i }[/math] are differentiable functions, [math]\displaystyle{ \mathbf{w}=(\mathbf{w}^1,...,\mathbf{w}^m) }[/math] is an [math]\displaystyle{ m }[/math]-dimensional standard Wiener process, [math]\displaystyle{ \theta \in \mathbb{R}^p }[/math] is a vector of [math]\displaystyle{ p }[/math] parameters, [math]\displaystyle{ \{\mathbf{e}_{t_k} : \mathbf{e}_{t_k}\sim \Nu ( 0,\Pi_{t_k}) \}_{k=0,...,M-1} }[/math] is a sequence of [math]\displaystyle{ r }[/math]-dimensional i.i.d. Gaussian random vectors independent of [math]\displaystyle{ \mathbf{w} }[/math], [math]\displaystyle{ \Pi_{t_k} }[/math] an [math]\displaystyle{ r \times r }[/math] positive definite matrix, and [math]\displaystyle{ \mathbf{C} }[/math] an [math]\displaystyle{ r \times d }[/math] matrix.
Statistical problem to solve
Once the dynamics of a phenomenon is described by a state equation as (1) and the way of measurement the state variables specified by an observation equation as (2), the inference problem to solve is the following:[1][3] given [math]\displaystyle{ M }[/math] partial and noisy observations [math]\displaystyle{ \mathbf{z}_{t_0},...,\mathbf{z}_{t_{M-1}} }[/math] of the stochastic process [math]\displaystyle{ \mathbf{x} }[/math] on the observation times [math]\displaystyle{ t_0,...,t_{M-1} }[/math], estimate the unobserved state variable of [math]\displaystyle{ \mathbf{x} }[/math] and the unknown parameters [math]\displaystyle{ \theta }[/math] in (1) that better fit to the given observations.
Discrete-time innovation process
Let [math]\displaystyle{ \{t\}_M }[/math] be the sequence of [math]\displaystyle{ M }[/math] observation times [math]\displaystyle{ t_0,\ldots,t_{M-1} }[/math] of the states of (1), and [math]\displaystyle{ Z_\rho =\{ \mathbf{z}_{t_k} : t_k\leq \rho, t_k \in \{ t \}_M \} }[/math] the time series of partial and noisy measurements of [math]\displaystyle{ \mathbf{x} }[/math] described by the observation equation (2).
Further, let [math]\displaystyle{ \mathbf{x}_{t/\rho} = \Epsilon (\mathbf{x}(t)|Z_\rho) }[/math] and [math]\displaystyle{ \mathbf{U}_{t/\rho }=E(\mathbf{x}(t)\mathbf{x}^{\intercal }(t)|Z_{\rho })-\mathbf{x}_{t/\rho }\mathbf{x}_{t/\rho }^{\intercal } }[/math] be the conditional mean and variance of [math]\displaystyle{ \mathbf{x} }[/math] with [math]\displaystyle{ \rho \leq t }[/math], where [math]\displaystyle{ E (\cdot) }[/math] denotes the expected value of random vectors.
The random sequence [math]\displaystyle{ \{ \nu_{t_k}\} _{k=1,\ldots,M-1}, }[/math] with
[math]\displaystyle{ \qquad \qquad \nu_{t_k} = \mathbf{z}_{t_k}- \mathbf{Cx}_{{t_k}/{t_{k-1}}}(\theta), \qquad \qquad (3) }[/math]
defines the discrete-time innovation process,[4][1][5] where [math]\displaystyle{ \nu_{t_k} }[/math] is proved to be an independent normally distributed random vector with zero mean and variance
[math]\displaystyle{ \qquad \qquad \Sigma_{t_k}= \mathbf{CU}_{{t_k}/t_{k-1}}(\theta)\ \mathbf{C}^\intercal + \Pi_{t_k}, \qquad \qquad (4) }[/math]
for small enough [math]\displaystyle{ \Delta=\underset{k}{\max } \{t_{k+1}-t_k\} }[/math], with [math]\displaystyle{ t_k,t_{k+1} \in \{t\}_{M} }[/math]. In practice,[6] this distribution for the discrete-time innovation is valid when, with a suitable selection of both, the number [math]\displaystyle{ M }[/math] of observations and the time distance [math]\displaystyle{ t_{k+1}-t_k }[/math] between consecutive observations, the time series of observations [math]\displaystyle{ \mathbf{z}_{t_0},...,\mathbf{z}_{t_{M-1}} }[/math] of the SDE contains the main information about the continuous-time process [math]\displaystyle{ \mathbf{x} }[/math]. That is, when the sampling of the continuous-time process [math]\displaystyle{ \mathbf{x} }[/math] has low distortion (aliasing) and when there is a suitable signal-noise ratio.
Innovation estimator
The innovation estimator for the parameters of the SDE (1) is the one that maximizes the likelihood function of the discrete-time innovation process [math]\displaystyle{ \{\nu_{t_k}\}_ {k=1,\ldots,M-1} }[/math] with respect to the parameters.[1] More precisely, given [math]\displaystyle{ M }[/math] measurements [math]\displaystyle{ Z_{t_{M-1}} }[/math]of the state space model (1)-(2) with [math]\displaystyle{ \theta = \theta_0 }[/math] on [math]\displaystyle{ \{t\}_M, }[/math] the innovation estimator for the parameters [math]\displaystyle{ \theta_0 }[/math] of (1) is defined by
[math]\displaystyle{ \qquad\qquad \hat{\theta}_M = \operatorname\arg\{\underset{\theta}{\min} \ U_M(\theta, Z_{t_{M-1}})\}, \qquad\qquad (5) }[/math]
where
[math]\displaystyle{ \qquad\qquad U_M(\theta,Z_{t_{M-1}}) = (M-1)\ln(2\pi)+\sum_{k=1}^{M-1} \ln(\det(\Sigma_{t_k})) + \nu_{t_k}^\intercal\Sigma_{t_k}^{-1}\nu_{t_k}, }[/math]
being [math]\displaystyle{ \nu_{t{_k}} }[/math]the discrete-time innovation (3) and [math]\displaystyle{ \Sigma_{t_k} }[/math]the innovation variance (4) of the model (1)-(2) at [math]\displaystyle{ t_k }[/math], for all [math]\displaystyle{ k=1,...,M-1. }[/math] In the above expression for [math]\displaystyle{ U_M (\theta, Z_{t_{M-1}}), }[/math] the conditional mean [math]\displaystyle{ \mathbf{x}_{t_k/t_{k-1}}(\theta) }[/math] and variance [math]\displaystyle{ \mathbf{U}_{t_k/t_{k-1}}(\theta) }[/math] are computed by the continuous-discrete filtering algorithm for the evolution of the moments (Section 6.4 in[2]), for all [math]\displaystyle{ k=1,...,M-1. }[/math]
Differences with the maximum likelihood estimator
The maximum likelihood estimator of the parameters [math]\displaystyle{ \theta }[/math] in the model (1)-(2) involves the evaluation of the - usually unknown - transition density function [math]\displaystyle{ p_\theta (t_{k+1}- t_k, \mathbf{x}(t_k), \mathbf{x}(t_{k+1})) }[/math] between the states [math]\displaystyle{ \mathbf{x}(t_k) }[/math] and [math]\displaystyle{ \mathbf{x}(t_{k+1}) }[/math] of the diffusion process [math]\displaystyle{ \mathbf{x} }[/math] for all the observation times [math]\displaystyle{ t_k }[/math] and [math]\displaystyle{ t_{k+1} }[/math].[7] Instead of this, the innovation estimator (5) is obtained by maximizing the likelihood of the discrete-time innovation process [math]\displaystyle{ \{ \nu_{t_k} \}_{k=1,...,M-1} , }[/math] taking into account that [math]\displaystyle{ \nu _{t_1},...,\nu _{t_{M-1}} }[/math] are Gaussian and independent random vectors. Remarkably, whereas the transition density function [math]\displaystyle{ p_{\theta}(t_{k+1}-t_k, \mathbf{x}(t_k),\mathbf{x}(t_{k+1})) }[/math] changes when the SDE for [math]\displaystyle{ \mathbf{x} }[/math] does, the transition density function [math]\displaystyle{ \mathfrak{p}_\theta(t_{k+1}-t_k, \nu_{t_{k}},\nu_{t_{k+1}} ) }[/math] for the innovation process remains Gaussian independently of the SDEs for [math]\displaystyle{ \mathbf{x} }[/math]. Only in the case that the diffusion [math]\displaystyle{ \mathbf{x} }[/math] is described by a linear SDE with additive noise, the density function [math]\displaystyle{ p_\theta(t_{k+1}-t_k, \mathbf{x}(t_k),\mathbf{x}(t_{k+1})) }[/math] is Gaussian and equal to [math]\displaystyle{ \mathfrak{p}_\theta(t_{k+1}-t_k, \nu_{t_k}, \nu_{t_{k+1}}), }[/math] and so the maximum likelihood and the innovation estimator coincide.[5] Otherwise,[5] the innovation estimator is an approximation to the maximum likelihood estimator and, in this sense, the innovation estimator is a Quasi-Maximum Likelihood estimator. In addition, the innovation method is a particular instance of the Prediction Error method according to the definition given in.[8] Therefore, the asymptotic results obtained in for that general class of estimators are valid for the innovation estimators.[1][9][10] Intuitively, by following the typical control engineering viewpoint, it is expected that the innovation process - viewed as a measure of the prediction errors of the fitted model - be approximately a white noise process when the models fit the data,[11][3] which can be used as a practical tool for designing of models and for optimal experimental design.[6]
Properties
The innovation estimator (5) has a number of important attributes:
- Under conventional regularity conditions, the innovation estimator (5) is consistent and asymptoticaly normal distributed.[1][10][12]
- For selecting models,[11] the maximum log-likelihood [math]\displaystyle{ -U_{M,h} ( \widehat{\theta}_M, Z_{t_{M-1}} ) }[/math] of the innovation estimator (5) can be used to compute the Akaike or Bayesian information criterion.
- The [math]\displaystyle{ 100 (1-\alpha)\% }[/math] confidence limits [math]\displaystyle{ \widehat{\theta}_M\pm\bigtriangleup }[/math] for the innovation estimator [math]\displaystyle{ \widehat{\theta}_M }[/math] is estimated with[6]
[math]\displaystyle{ \ \qquad \qquad \bigtriangleup = t_{1-\alpha, M-\rho-1}\sqrt{\frac{diag(Var(\widehat{\theta}_M))}{M-p}}, }[/math]
where [math]\displaystyle{ t_{1-\alpha, M-p-1} }[/math] is the t-student distribution with [math]\displaystyle{ 100 (1-\alpha)\% }[/math] significance level, and [math]\displaystyle{ M-p-1 }[/math] degrees of freedom . Here, [math]\displaystyle{ \text{V} ar (\widehat{\theta}_M)= (I (\widehat{\theta}_M))^{-1} }[/math] denotes the variance of the innovation estimator [math]\displaystyle{ \widehat{\theta}_M }[/math], where
[math]\displaystyle{ \ \qquad \qquad I(\widehat{\theta }_{M})=\sum_{k=1}^{M-1}I_{k}(\widehat{\theta }_{M}) }[/math]
is the Fisher Information matrix the innovation estimator [math]\displaystyle{ \widehat{\theta }_{M} }[/math] of [math]\displaystyle{ \theta _{0} }[/math] and
[math]\displaystyle{ \qquad \qquad \lbrack I_{k}(\widehat{\theta }_{M})]_{m,n}=\frac{\partial \mu ^{\intercal }}{\partial \theta _{m}}\Sigma ^{-1}\frac{\partial \mu }{\partial \theta _{n}} +\frac{1}{2}trace(\Sigma ^{-1}\frac{\partial \Sigma }{\partial \theta _{m}}\Sigma ^{-1}\frac{\partial \Sigma }{\partial \theta _{n}}) }[/math]
is the entry [math]\displaystyle{ (m,n) }[/math] of the matrix [math]\displaystyle{ I_{k}(\widehat{\theta }_{M}) }[/math] with [math]\displaystyle{ \mu = \mathbf{Cx}_{t_{k}/t_{k-1}}(\widehat{\theta }_{M}) }[/math] and [math]\displaystyle{ \Sigma =\mathbf{\Sigma }_{t_{k}}(\widehat{\theta }_{M}) }[/math], for [math]\displaystyle{ 1\leq m,n\leq p }[/math].
- The distribution of the fitting-innovation process [math]\displaystyle{ \{\mathbf{\nu }_{t_{k}}:\mathbf{\nu }_{t_{k}}=\mathbf{z}_{t_{k}}-\mathbf{Cx} _{t_{k}/t_{k-1}}(\widehat{\theta }_{M})\}_{k=1,\ldots M-1} }[/math] measures the goodness of fit of the model to the data.[1][3][11][6]
- For smooth enough function [math]\displaystyle{ \mathbf{h} }[/math], nonlinear observation equations of the form
[math]\displaystyle{ \qquad \qquad \mathbf{z}_{t_{k}}=\mathbf{h}(t_{k}\text{, }\mathbf{x}(t_{k}))+\mathbf{e}_{t_{k}}, \qquad \qquad (6) }[/math]
can be transformed to the simpler one (2), and the innovation estimator (5) can be applied.[5]
Approximate Innovation estimators
In practice, close form expressions for computing [math]\displaystyle{ \mathbf{x}_{t_{k}/t_{k-1}}(\theta ) }[/math] and [math]\displaystyle{ \mathbf{U}_{t_{k}/t_{k-1}}(\theta ) }[/math] in (5) are only available for a few models (1)-(2). Therefore, approximate filtering algorithms as the following are used in applications.
Given [math]\displaystyle{ M }[/math] measurements [math]\displaystyle{ Z_{t_{M-1}} }[/math] and the initial filter estimates [math]\displaystyle{ \mathbf{y}_{t_{0}/t_{0}}=\mathbf{x}_{t_{0}/t_{0}} }[/math], [math]\displaystyle{ \mathbf{V}_ {t_{0}/t_{0}}=\mathbf{U}_{t_{0}/t_{0}} }[/math], the approximate Linear Minimum Variance (LMV) filter for the model (1)-(2) is iteratively defined at each observation time [math]\displaystyle{ t_{k}\in \{t\}_{M} }[/math] by the prediction estimates[2][13]
[math]\displaystyle{ \qquad \qquad \mathbf{y}_{t_{k+1}/t_{k}}=E(\mathbf{y}(t_{k+1})|Z_{t_{k}}) \quad }[/math] and [math]\displaystyle{ \quad \mathbf{V}_{t_{k+1}/t_{k}}=E(\mathbf{y}(t_{k+1})\mathbf{y} ^{\intercal }(t_{k+1})|Z_{t_{k}})-\mathbf{y}_{t_{k+1}/t_{k}}\mathbf{y}_{t_{k+1}/t_{k}}^{\intercal }, \qquad (7) }[/math]
with initial conditions [math]\displaystyle{ \mathbf{y}_{t_{k}/t_{k}} }[/math] and [math]\displaystyle{ \mathbf{V}_{t_{k}/t_{k}} }[/math], and the filter estimates
[math]\displaystyle{ \qquad \qquad \mathbf{y}_{t_{k+1}/t_{k+1}}=\mathbf{y}_{t_{k+1}/t_{k}}+\mathbf{K}_{t_{k+1}} \mathbf{(\mathbf{z}}_{t_{k+1}}-\mathbf{\mathbf{C}y}_{t_{k+1}/t_{k}}\mathbf{)} \quad }[/math] and [math]\displaystyle{ \quad \mathbf{V}_{t_{k+1}/t_{k+1}}=\mathbf{V}_{t_{k+1}/t_{k}}-\mathbf{K}_{t_{k+1}}\mathbf{CV}_{t_{k+1}/t_{k}} \qquad (8) }[/math]
with filter gain
[math]\displaystyle{ \qquad \qquad \mathbf{K}_{t_{k+1}}=\mathbf{V}_{t_{k+1}/t_{k}}\mathbf{C}^{\intercal } \mathbf{CV}_{t_{k+1}/t_{k}} (\mathbf{C}^{\intercal }+\mathbf{\Pi }_{t_{k+1}})^{-1} }[/math]
for all [math]\displaystyle{ t_{k},t_{k+1}\in \{t\}_{M} }[/math], where [math]\displaystyle{ \mathbf{y} }[/math] is an approximation to the solution [math]\displaystyle{ \mathbf{x} }[/math] of (1) on the observation times [math]\displaystyle{ \{t\}_{M} }[/math].
Given [math]\displaystyle{ M }[/math] measurements [math]\displaystyle{ Z_{t_{M-1}} }[/math] of the state space model (1)-(2) with [math]\displaystyle{ \mathbf{\theta =\theta }_{0} }[/math] on [math]\displaystyle{ \{t\}_{M} }[/math], the approximate innovation estimator for the parameters [math]\displaystyle{ \mathbf{\theta }_{0} }[/math] of (1) is defined by[1][12]
[math]\displaystyle{ \qquad \qquad \widehat{\mathbf{\vartheta }}_{M}=\arg \{\underset{\mathbf{\theta \in } \mathcal{D}_{\theta }}{\mathbf{\min }}\text{ }\widetilde{U}_{M}\mathbf{(\theta },Z_{t_{M-1}})\}, \qquad \qquad (9) }[/math]
where
[math]\displaystyle{ \qquad \qquad \widetilde{U}_{M}(\mathbf{\theta },Z_{t_{M-1}})=(M-1)\ln (2\pi)+\sum\limits_{k=1}^{M-1}\ln (\det (\widetilde{\mathbf{\Sigma }}_{t_{k}}))+\widetilde{\mathbf{\nu }}_{t_{k}}^{\intercal }(\widetilde{\mathbf{\Sigma }}_{t_{k}})^{-1}\widetilde{\mathbf{\nu }}_{t_{k}}, }[/math]
being
[math]\displaystyle{ \qquad \qquad \widetilde{\mathbf{\nu }}_{t_{k}}=\mathbf{z}_{t_{k}}-\mathbf{Cy}_{t_{k}/t_{k-1}}(\theta ) \qquad }[/math] and [math]\displaystyle{ \qquad \widetilde{\mathbf{\Sigma }}_{t_{k}}=\mathbf{CV}_{t_{k}/t_{k-1}}(\theta )\mathbf{C}^{\intercal }+\mathbf{\Pi }_{t_{k}} }[/math]
approximations to the discrete-time innovation (3) and innovation variance (4), respectively, resulting from the filtering algorithm (7)-(8).
For models with complete observations free of noise (i.e., with [math]\displaystyle{ \mathbf{C}=\mathbf{I} }[/math] and [math]\displaystyle{ \mathbf{\Pi }_{t_{k}}=0 }[/math] in (2)), the approximate innovation estimator (9) reduces to the known Quasi-Maximum Likelihood estimators for SDEs.[12]
Main conventional-type estimators
Conventional-type innovation estimators are those (9) derived from conventional-type continuous-discrete or discrete-discrete approximate filtering algorithms. With approximate continuous-discrete filters there are the innovation estimators based on Local Linearization (LL) filters,[1][14][5] on the extended Kalman filter,[15][16] and on the second order filters.[3][16] Approximate innovation estimators based on discrete-discrete filters result from the discretization of the SDE (1) by means of a numerical scheme.[17][18] Typically, the effectiveness of these innovation estimators is directly related to the stability of the involved filtering algorithms.
A shared drawback of these conventional-type filters is that, once the observations are given, the error between the approximate and the exact innovation process is fixed and completely settled by the time distance between observations.[12] This might set a large bias of the approximate innovation estimators in some applications, bias that cannot be corrected by increasing the number of observations. However, the conventional-type innovation estimators are useful in many practical situations for which only medium or low accuracy for the parameter estimation is required.[12]
Order-β innovation estimators
Let us consider the finer time discretization [math]\displaystyle{ \left( \tau \right) _{h\gt 0}=\{\tau _{n}:\tau _{n+1}-\tau _{n}\leq h\text{ for }n=0,1,\ldots ,N\} }[/math] of the time interval [math]\displaystyle{ [t_{0},t_{M-1}] }[/math] satisfying the condition [math]\displaystyle{ \left( \tau\right) _{h}\supset \{t\}_{M} }[/math]. Further, let [math]\displaystyle{ \mathbf{y}_n }[/math] be the approximate value of [math]\displaystyle{ \mathbf{x}(\tau_n) }[/math] obtained from a discretization of the equation (1) for all [math]\displaystyle{ \left(\tau \right)_{h} }[/math], and
[math]\displaystyle{ \qquad \qquad \mathbf{y}=\{\mathbf{y}(t),t\in \lbrack t_{0},t_{M-1}] : \mathbf{y}(\tau _{n})=\mathbf{y}_{n}, \quad }[/math] for all [math]\displaystyle{ \quad \tau _{n}\in \left( \tau \right) _{h}\} \qquad \qquad (10) }[/math]
a continuous-time approximation to [math]\displaystyle{ \mathbf{x} }[/math].
A order-[math]\displaystyle{ \beta }[/math] LMV filter.[13] is an approximate LMV filter for which [math]\displaystyle{ \mathbf{y} }[/math] is an order-[math]\displaystyle{ \beta }[/math] weak approximation to [math]\displaystyle{ \mathbf{x} }[/math] satisfying (10) and the weak convergence condition
[math]\displaystyle{ \qquad \qquad \underset{t_{k}\leq t\leq t_{k+1}}{\sup }\left\vert E\left( g(\mathbf{x} (t))|Z_{t_{k}}\right) -E\left( g(\mathbf{y}(t))|Z_{t_{k}}\right) \right\vert \leq L_{k}h^{\beta } }[/math]
for all [math]\displaystyle{ t_{k},t_{k+1}\in \{t\}_{M} }[/math] and any [math]\displaystyle{ 2(\beta +1) }[/math] times continuously differentiable functions [math]\displaystyle{ g:\mathbb{R}^{d}\rightarrow \mathbb{R} }[/math] for which [math]\displaystyle{ g }[/math] and all its partial derivatives up to order [math]\displaystyle{ 2(\beta +1) }[/math] have polynomial growth, being [math]\displaystyle{ L_{k} }[/math] a positive constant. This order-[math]\displaystyle{ \beta }[/math] LMV filter converges with rate [math]\displaystyle{ \beta }[/math] to the exact LMV filter as [math]\displaystyle{ h }[/math] goes to zero,[13] where [math]\displaystyle{ h }[/math] is the maximum stepsize of the time discretization [math]\displaystyle{ (\tau )_{h}\supset \{t\}_{M} }[/math] on which the approximation [math]\displaystyle{ \mathbf{y} }[/math] to [math]\displaystyle{ \mathbf{x} }[/math] is defined.
A order-[math]\displaystyle{ \beta }[/math] innovation estimator is an approximate innovation estimator (9) for which the approximations to the discrete-time innovation (3) and innovation variance (4), respectively, resulting from an order-[math]\displaystyle{ \beta }[/math] LMV filter.[12]
Approximations [math]\displaystyle{ \mathbf{y} }[/math] of any kind converging to [math]\displaystyle{ \mathbf{x} }[/math] in a weak sense (as, e.g., those in [19][13]) can be used to design an order-[math]\displaystyle{ \beta }[/math] LMV filter and, consequently, an order-[math]\displaystyle{ \beta }[/math] innovation estimator. These order-[math]\displaystyle{ \beta }[/math] innovation estimators are intended for the recurrent practical situation in which a diffusion process should be identified from a reduced number of observations distant in time or when high accuracy for the estimated parameters is required.
Properties
An order-[math]\displaystyle{ \beta }[/math] innovation estimator [math]\displaystyle{ \widehat{\mathbf{\theta }}_{M}(h) }[/math] has a number of important properties:[12][6]
- For each given data [math]\displaystyle{ Z_{t_{M-1}} }[/math] of [math]\displaystyle{ M }[/math] observations, [math]\displaystyle{ \widehat{\mathbf{\theta }}_{M}(h) }[/math] converges to the exact innovation estimator [math]\displaystyle{ \widehat{\mathbf{\theta }}_{M} }[/math] as the maximum stepsize [math]\displaystyle{ h }[/math] of the time discretization [math]\displaystyle{ \left( \tau \right) _{h}\supset \{t\}_{M} }[/math] goes to zero.
- For finite samples of [math]\displaystyle{ M }[/math] observations, the expected value of [math]\displaystyle{ \widehat{\mathbf{\theta }}_{M}(h) }[/math] converges to the expected value of the exact innovation estimator [math]\displaystyle{ \widehat{\mathbf{\theta }}_{M} }[/math] as [math]\displaystyle{ h }[/math] goes to zero.
- For an increasing number of observations, [math]\displaystyle{ \widehat{\mathbf{\theta }}_{M}(h) }[/math] is asymptotically normal distributed and its bias decreases when [math]\displaystyle{ h }[/math] goes to zero.
- Likewise to the convergence of the order-[math]\displaystyle{ \beta }[/math] LMV filter to the exact LMV filter, for the convergence and asymptotic properties of [math]\displaystyle{ \widehat{\mathbf{\theta }}_{M}(h) }[/math] there are no constraints on the time distance [math]\displaystyle{ t_{k+1}-t_{k} }[/math] between two consecutive observations [math]\displaystyle{ \mathbf{z}_{t_{k}} }[/math] and [math]\displaystyle{ \mathbf{z}_{t_{k+1}} }[/math], nor on the time discretization [math]\displaystyle{ (\tau )_{h} \supset \{t\}_{M}. }[/math]
- Approximations for the Akaike or Bayesian information criterion and confidence limits are directly obtained by replacing the exact estimator [math]\displaystyle{ \widehat{\mathbf{\theta }}_{M} }[/math] by its approximation [math]\displaystyle{ \widehat{\mathbf{\theta }}_{M}(h) }[/math]. These approximations converge to the corresponding exact one when the maximum stepsize [math]\displaystyle{ h }[/math] of the time discretization [math]\displaystyle{ \left( \tau \right) _{h}\supset \{t\}_{M} }[/math] goes to zero.
- The distribution of the approximate fitting-innovation process [math]\displaystyle{ \{\widetilde{\mathbf{\nu }}_{t_{k}}:\widetilde{\mathbf{\nu }}_{t_{k}}=\mathbf{z}_{t_{k}}-\mathbf{Cy}_{t_{k}/t_{k-1}}(\widehat{\theta }_{M}(h))\}_{k=1,\ldots M-1} }[/math] measures the goodness of fit of the model to the data, which is also used as a practical tool for designing of models and for optimal experimental design.
- For smooth enough function [math]\displaystyle{ \mathbf{h} }[/math], nonlinear observation equations of the form (6) can be transformed to the simpler one (2), and the order-[math]\displaystyle{ \beta }[/math] innovation estimator can be applied.

Figure 1 presents the histograms of the differences [math]\displaystyle{ (\widehat{\alpha }_{M}-\widehat{\alpha}^D_{h,M},\widehat{\sigma}_{M}-\widehat{\sigma}^D_{h,M}) }[/math] and [math]\displaystyle{ (\widehat{\alpha }_{M}-\widehat{\alpha}_{h,M},\widehat{\sigma}_{M}-\widehat{\sigma}_{h,M}) }[/math] between the exact innovation estimator [math]\displaystyle{ (\widehat{\alpha }_{M},\widehat{\sigma}_{M}) }[/math] with the conventional [math]\displaystyle{ (\widehat{\alpha}^D_{h,M},\widehat{\sigma}^D_{h,M}) }[/math] and order-[math]\displaystyle{ 1 }[/math] [math]\displaystyle{ (\widehat{\alpha}_{h,M},\widehat{\sigma}_{h,M}) }[/math] innovation estimators for the parameters [math]\displaystyle{ \alpha =-0.1 }[/math] and [math]\displaystyle{ \sigma = 0.1 }[/math] of the equation[12]
[math]\displaystyle{ \qquad dx = txdt + \sigma \sqrt{t}x dw \quad (11) }[/math]
obtained from 100 time series [math]\displaystyle{ z_{t_{0}},..,z_{t_{M-1}} }[/math] of [math]\displaystyle{ M }[/math] noisy observations
[math]\displaystyle{ \qquad z_{t_{k}}=x(t_{k})+e_{t_{k}},\text{ for }k=0,1,..,M-1, \quad (12) }[/math]
of [math]\displaystyle{ x }[/math] on the observation times [math]\displaystyle{ \{t\}_{M=10}=\{t_{k}=0.5+k\Delta :k=0,\ldots M-1 }[/math], [math]\displaystyle{ \Delta =1\} }[/math], with [math]\displaystyle{ x(0.5)=1 }[/math] and [math]\displaystyle{ \Pi _{k}=0.0001 }[/math]. The classical and the order-[math]\displaystyle{ 1 }[/math] Local Linearization filters of the innovation estimators [math]\displaystyle{ (\widehat{\alpha}^D_{h,M},\widehat{\sigma}^D_{h,M}) }[/math] and [math]\displaystyle{ (\widehat{\alpha}_{h,M},\widehat{\sigma}_{h,M}) }[/math] are defined as in,[12] respectively, on the uniform time discretizations [math]\displaystyle{ \left( \tau \right) _{h=\Delta}\equiv \{t\}_{M} }[/math] and [math]\displaystyle{ \left( \tau \right)_{h=\Delta/2,\Delta/8,\Delta/32}=\{\tau _{n}:\tau _{n}=0.5+nh }[/math], with [math]\displaystyle{ n=0,1,\ldots ,(M-1)/h\} }[/math]. The number of stochastic simulations of the order-[math]\displaystyle{ 1 }[/math] Local Linearization filter is estimated via an adaptive sampling algorithm with moderate tolerance. The Figure 1 illustrates the convergence of the order-[math]\displaystyle{ 1 }[/math] innovation estimator [math]\displaystyle{ (\widehat{\alpha}_{h,M},\widehat{\sigma}_{h,M}) }[/math] to the exact innovation estimators [math]\displaystyle{ (\widehat{\alpha }_{M},\widehat{\sigma}_{M}) }[/math] as [math]\displaystyle{ h }[/math] decreases, which substantially improves the estimation provided by the conventional innovation estimator [math]\displaystyle{ (\widehat{\alpha}^D_{\Delta,M},\widehat{\sigma}^D_{\Delta,M}) }[/math].
Deterministic approximations
The order-[math]\displaystyle{ \beta }[/math] innovation estimators overcome the drawback of the conventional-type innovation estimators concerning the impossibility of reducing bias.[12] However, the viable bias reduction of an order-[math]\displaystyle{ \beta }[/math] innovation estimators might eventually require that the associated order-[math]\displaystyle{ \beta }[/math] LMV filter performs a large number of stochastic simulations.[13] In situations where only low or medium precision approximate estimators are needed, an alternative deterministic filter algorithm - called deterministic order-[math]\displaystyle{ \beta }[/math] LMV filter [13] - can be obtained by tracking the first two conditional moments [math]\displaystyle{ \mu }[/math] and [math]\displaystyle{ \Lambda }[/math] of the order-[math]\displaystyle{ \beta }[/math] weak approximation [math]\displaystyle{ \mathbf{y} }[/math] at all the time instants [math]\displaystyle{ \tau _{n}\in \left( \tau \right) _{h} }[/math] in between two consecutive observation times [math]\displaystyle{ t_{k} }[/math] and [math]\displaystyle{ t_{k+1} }[/math]. That is, the value of the predictions [math]\displaystyle{ \mathbf{y}_{t_{k+1}/t_{k}} }[/math] and [math]\displaystyle{ \mathbf{P}_{t_{k+1}/t_{k}} }[/math] in the filtering algorithm are computed from the recursive formulas
[math]\displaystyle{ \qquad \qquad \mathbf{y}_{\tau _{n+1}/t_{k}}=\mu (\tau _{n},\mathbf{y}_{\tau_{n}/t_{k}};h_{n})\quad }[/math] and [math]\displaystyle{ \quad \mathbf{P}_{\tau_{n+1}/t_{k}}=\Lambda (\tau _{n},\mathbf{P}_{\tau _{n}/t_{k}};h_{n}),\quad }[/math] with [math]\displaystyle{ \tau _{n},\tau _{n+1}\in (\tau )_{h}\cap \lbrack t_{k,}t_{k+1}], }[/math]
and with [math]\displaystyle{ h_n=\tau _{n+1}-\tau _{n} }[/math]. The approximate innovation estimators [math]\displaystyle{ \widehat{\mathbf{\theta }}_{h,M} }[/math] defined with these deterministic order-[math]\displaystyle{ \beta }[/math] LMV filters not longer converge to the exact innovation estimator, but allow a significant bias reduction in the estimated parameters for a given finite sample with a lower computational cost.
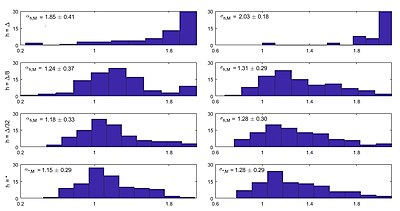
Figure 2 presents the histograms and the confidence limits of the approximate innovation estimators [math]\displaystyle{ (\widehat{\alpha }_{h,M},\widehat{\sigma }_{h,M}) }[/math] and [math]\displaystyle{ (\widehat{\alpha }_{\cdot ,M},\widehat{\sigma }_{\cdot ,M}) }[/math] for the parameters [math]\displaystyle{ \alpha =1 }[/math] and [math]\displaystyle{ \sigma =1 }[/math] of the Van der Pol oscillator with random frequency[12]
[math]\displaystyle{ \qquad dx_{1} =x_{2} dt \quad (13) }[/math]
[math]\displaystyle{ \qquad dx_{2} =(-(x_{1}^{2}-1)x_{2}-\alpha x_{1})dt+\sigma x_{1}dw \quad (14) }[/math]
obtained from 100 time series [math]\displaystyle{ z_{t_{0}},..,z_{t_{M-1}} }[/math] of [math]\displaystyle{ M }[/math] partial and noisy observations
[math]\displaystyle{ \qquad z_{t_{k}}=x_{1}(t_{k})+e_{t_{k}},\text{ for }k=0,1,..,M-1, \quad (15) }[/math]
of [math]\displaystyle{ x }[/math] on the observation times [math]\displaystyle{ \{t\}_{M=30}=\{t_{k}=k\Delta :k=0,\ldots M-1 }[/math], [math]\displaystyle{ \Delta =1\} }[/math], with [math]\displaystyle{ (x_{1}(0),x_{1}(0))=(1,1) }[/math] and [math]\displaystyle{ \Pi _{k}=0.001 }[/math]. The deterministic order-[math]\displaystyle{ 1 }[/math] Local Linearization filter of the innovation estimators [math]\displaystyle{ (\widehat{\alpha }_{h,,M},\widehat{\sigma }_{h,M}) }[/math] and [math]\displaystyle{ (\widehat{\alpha }_{\cdot ,M},\widehat{\sigma }_{\cdot ,M}) }[/math] is defined,[12] for each estimator, on uniform time discretizations [math]\displaystyle{ \left( \tau\right) _{h}=\{\tau _{n}:\tau _{n}=nh }[/math], with [math]\displaystyle{ n=0,1,\ldots ,(M-1)/h\} }[/math] and on an adaptive time-stepping discretization [math]\displaystyle{ \left( \tau \right) _{\cdot } }[/math] with moderate relative and absolute tolerances, respectively. Observe the bias reduction of the estimated parameter as [math]\displaystyle{ h }[/math] decreases.
Software
A Matlab implementation of various approximate innovation estimators is provided by the SdeEstimation toolbox.[20] This toolbox has Local Linearization filters, including deterministic and stochastic options with fixed step sizes and sample numbers. It also offers adaptive time stepping and sampling algorithms, along with local and global optimization algorithms for innovation estimation. For models with complete observations free of noise, various approximations to the Quasi-Maximum Likelihood estimator are implemented in R.[21]
References
- ↑ 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 Ozaki, Tohru (1994), Bozdogan, H.; Sclove, S. L.; Gupta, A. K. et al., eds., "The Local Linearization Filter with Application to Nonlinear System Identifications" (in en), Proceedings of the First US/Japan Conference on the Frontiers of Statistical Modeling: An Informational Approach: Volume 3 Engineering and Scientific Applications (Dordrecht: Springer Netherlands): pp. 217–240, doi:10.1007/978-94-011-0854-6_10, ISBN 978-94-011-0854-6, https://doi.org/10.1007/978-94-011-0854-6_10, retrieved 2023-07-06
- ↑ 2.0 2.1 2.2 2.3 Jazwinski A.H., Stochastic Processes and Filtering Theory, Academic Press, New York, 1970.
- ↑ 3.0 3.1 3.2 3.3 Nielsen, Jan Nygaard; Vestergaard, Martin (2000). "Estimation in continuous-time stochastic volatility models using nonlinear filters". International Journal of Theoretical and Applied Finance 03 (2): 279–308. doi:10.1142/S0219024900000139. ISSN 0219-0249. https://www.worldscientific.com/doi/abs/10.1142/S0219024900000139.
- ↑ Kailath T., Lectures on Wiener and Kalman Filtering. New York: Springer-Verlag, 1981.
- ↑ 5.0 5.1 5.2 5.3 5.4 Jimenez, J. C.; Ozaki, T. (2006). "An Approximate Innovation Method For The Estimation Of Diffusion Processes From Discrete Data" (in en). Journal of Time Series Analysis 27 (1): 77–97. doi:10.1111/j.1467-9892.2005.00454.x. ISSN 0143-9782. https://onlinelibrary.wiley.com/doi/10.1111/j.1467-9892.2005.00454.x.
- ↑ 6.0 6.1 6.2 6.3 6.4 Jimenez, J. C.; Yoshimoto, A.; Miwakeichi, F. (2021-08-24). "State and parameter estimation of stochastic physical systems from uncertain and indirect measurements" (in en). The European Physical Journal Plus 136 (8): 136, 869. doi:10.1140/epjp/s13360-021-01859-1. ISSN 2190-5444. Bibcode: 2021EPJP..136..869J. https://doi.org/10.1140/epjp/s13360-021-01859-1.
- ↑ Schweppe, F. (1965). "Evaluation of likelihood functions for Gaussian signals". IEEE Transactions on Information Theory 11 (1): 61–70. doi:10.1109/TIT.1965.1053737. ISSN 1557-9654. https://ieeexplore.ieee.org/document/1053737.
- ↑ Ljung L., System Identification, Theory for the User (2nd edn). Englewood Cliffs: Prentice Hall, 1999.
- ↑ Lennart, Ljung; Caines, Peter E. (1980). "Asymptotic normality of prediction error estimators for approximate system models" (in en). Stochastics 3 (1–4): 29–46. doi:10.1080/17442507908833135. ISSN 0090-9491. http://www.tandfonline.com/doi/abs/10.1080/17442507908833135.
- ↑ 10.0 10.1 Nolsoe K., Nielsen, J.N., Madsen H. (2000) "Prediction-based estimating function for diffusion processes with measurement noise", Technical Reports 2000, No. 10, Informatics and Mathematical Modelling, Technical University of Denmark.
- ↑ 11.0 11.1 11.2 Ozaki, T.; Jimenez, J. C.; Haggan-Ozaki, V. (2000). "The Role of the Likelihood Function in the Estimation of Chaos Models" (in en). Journal of Time Series Analysis 21 (4): 363–387. doi:10.1111/1467-9892.00189. ISSN 0143-9782. https://onlinelibrary.wiley.com/doi/10.1111/1467-9892.00189.
- ↑ 12.00 12.01 12.02 12.03 12.04 12.05 12.06 12.07 12.08 12.09 12.10 12.11 Jimenez, J.C. (2020). "Bias reduction in the estimation of diffusion processes from discrete observations". IMA Journal of Mathematical Control and Information 37 (4): 1468–1505. doi:10.1093/imamci/dnaa021. https://academic.oup.com/imamci/article/37/4/1468/5903959. Retrieved 2023-07-06.
- ↑ 13.0 13.1 13.2 13.3 13.4 13.5 Jimenez, J.C. (2019). "Approximate linear minimum variance filters for continuous-discrete state space models: convergence and practical adaptive algorithms". IMA Journal of Mathematical Control and Information 36 (2): 341–378. doi:10.1093/imamci/dnx047. https://academic.oup.com/imamci/article/36/2/341/4634018. Retrieved 2023-07-06.
- ↑ Shoji, Isao (1998). "A comparative study of maximum likelihood estimators for nonlinear dynamical system models" (in en). International Journal of Control 71 (3): 391–404. doi:10.1080/002071798221731. ISSN 0020-7179. https://www.tandfonline.com/doi/full/10.1080/002071798221731.
- ↑ Nielsen, Jan Nygaard; Madsen, Henrik (2001-01-01). "Applying the EKF to stochastic differential equations with level effects" (in en). Automatica 37 (1): 107–112. doi:10.1016/S0005-1098(00)00128-X. ISSN 0005-1098. https://www.sciencedirect.com/science/article/pii/S000510980000128X.
- ↑ 16.0 16.1 Singer, Hermann (2002). "Parameter Estimation of Nonlinear Stochastic Differential Equations: Simulated Maximum Likelihood versus Extended Kalman Filter and Itô-Taylor Expansion" (in en). Journal of Computational and Graphical Statistics 11 (4): 972–995. doi:10.1198/106186002808. ISSN 1061-8600. http://www.tandfonline.com/doi/abs/10.1198/106186002808.
- ↑ Ozaki, Tohru; Iino, Mitsunori (2001). "An innovation approach to non-Gaussian time series analysis" (in en). Journal of Applied Probability 38 (A): 78–92. doi:10.1239/jap/1085496593. ISSN 0021-9002. https://www.cambridge.org/core/journals/journal-of-applied-probability/article/abs/an-innovation-approach-to-nongaussian-time-series-analysis/B22EEB7243BC878CEB6DA367B0EEE7F5.
- ↑ Peng, H.; Ozaki, T.; Jimenez, J.C. (2002). "Modeling and control for foreign exchange based on a continuous time stochastic microstructure model". Proceedings of the 41st IEEE Conference on Decision and Control, 2002. 4. pp. 4440–4445 vol.4. doi:10.1109/CDC.2002.1185071. ISBN 0-7803-7516-5. https://ieeexplore.ieee.org/document/1185071.
- ↑ Kloeden P.E., Platen E., Numerical Solution of Stochastic Differential Equations, 3rd edn. Berlin: Springer, 1999.
- ↑ "GitHub - locallinearization/SdeEstimation" (in en). https://github.com/locallinearization/SdeEstimation.
- ↑ Iacus S.M., Simulation and inference for stochastic differential equations: with R examples, New York: Springer, 2008.
 |

