Zero-symmetric graph
In the mathematical field of graph theory, a zero-symmetric graph is a connected graph in which each vertex has exactly three incident edges and, for each two vertices, there is a unique symmetry taking one vertex to the other. Such a graph is a vertex-transitive graph but cannot be an edge-transitive graph: the number of symmetries equals the number of vertices, too few to take every edge to every other edge.[1]
The name for this class of graphs was coined by R. M. Foster in a 1966 letter to H. S. M. Coxeter.[2] In the context of group theory, zero-symmetric graphs are also called graphical regular representations of their symmetry groups.[3]
Examples
The smallest zero-symmetric graph is a nonplanar graph with 18 vertices.[4] Its LCF notation is [5,−5]9.
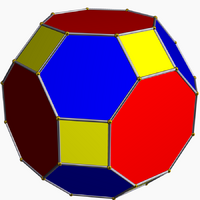
Among planar graphs, the truncated cuboctahedral and truncated icosidodecahedral graphs are also zero-symmetric.[5]
These examples are all bipartite graphs. However, there exist larger examples of zero-symmetric graphs that are not bipartite.[6]
These examples also have three different symmetry classes (orbits) of edges. However, there exist zero-symmetric graphs with only two orbits of edges. The smallest such graph has 20 vertices, with LCF notation [6,6,-6,-6]5.[7]
Properties
Every finite zero-symmetric graph is a Cayley graph, a property that does not always hold for cubic vertex-transitive graphs more generally and that helps in the solution of combinatorial enumeration tasks concerning zero-symmetric graphs. There are 97687 zero-symmetric graphs on up to 1280 vertices. These graphs form 89% of the cubic Cayley graphs and 88% of all connected vertex-transitive cubic graphs on the same number of vertices.[8]
| Unsolved problem in mathematics: Does every finite zero-symmetric graph contain a Hamiltonian cycle? (more unsolved problems in mathematics)
|
All known finite connected zero-symmetric graphs contain a Hamiltonian cycle, but it is unknown whether every finite connected zero-symmetric graph is necessarily Hamiltonian.[9] This is a special case of the Lovász conjecture that (with five known exceptions, none of which is zero-symmetric) every finite connected vertex-transitive graph and every finite Cayley graph is Hamiltonian.
See also
- Semi-symmetric graph, graphs that have symmetries between every two edges but not between every two vertices (reversing the roles of edges and vertices in the definition of zero-symmetric graphs)
References
- ↑ Zero-symmetric graphs, Academic Press, Inc. [Harcourt Brace Jovanovich, Publishers], New York-London, 1981, ISBN 0-12-194580-4
- ↑ (Coxeter Frucht), p. ix.
- ↑ Lauri, Josef; Scapellato, Raffaele (2003), Topics in Graph Automorphisms and Reconstruction, London Mathematical Society Student Texts, Cambridge University Press, pp. 66, ISBN 9780521529037, https://books.google.com/books?id=hsymFm0E0uIC&pg=PA66.
- ↑ (Coxeter Frucht), Figure 1.1, p. 5.
- ↑ (Coxeter Frucht), pp. 75 and 80.
- ↑ (Coxeter Frucht), p. 55.
- ↑ Conder, Marston D. E.; Pisanski, Tomaž; Žitnik, Arjana (2017), "Vertex-transitive graphs and their arc-types", Ars Mathematica Contemporanea 12 (2): 383–413, doi:10.26493/1855-3974.1146.f96
- ↑ Potočnik, Primož; Spiga, Pablo; Verret, Gabriel (2013), "Cubic vertex-transitive graphs on up to 1280 vertices", Journal of Symbolic Computation 50: 465–477, doi:10.1016/j.jsc.2012.09.002.
- ↑ (Coxeter Frucht), p. 10.
 |