Flat function
In mathematics, especially real analysis, a real function is flat at [math]\displaystyle{ x_0 }[/math] if all its derivatives at [math]\displaystyle{ x_0 }[/math] exist and equal 0.
A function that is flat at [math]\displaystyle{ x_0 }[/math] is not analytic at [math]\displaystyle{ x_0 }[/math] unless it is constant in a neighbourhood of [math]\displaystyle{ x_0 }[/math] (since an analytic function must equals the sum of its Taylor series).
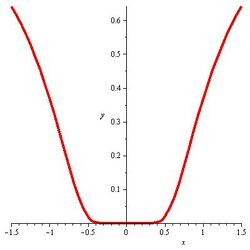
An example of a flat function at 0 is the function such that [math]\displaystyle{ f(0)=0 }[/math] and [math]\displaystyle{ f(x)=e^{-1/x^2} }[/math] for [math]\displaystyle{ x\neq 0. }[/math]
The function need not be flat at just one point. Trivially, constant functions on [math]\displaystyle{ \mathbb{R} }[/math] are flat everywhere. But there are also other, less trivial, examples; for example, the function such that [math]\displaystyle{ f(x)=0 }[/math] for [math]\displaystyle{ x\leq 0 }[/math] and [math]\displaystyle{ f(x)=e^{-1/x^2} }[/math] for [math]\displaystyle{ x\gt 0. }[/math]
Example
The function defined by
- [math]\displaystyle{ f(x) = \begin{cases} e^{-1/x^2} & \text{if }x\neq 0 \\ 0 & \text{if }x = 0 \end{cases} }[/math]
is flat at [math]\displaystyle{ x = 0 }[/math]. Thus, this is an example of a non-analytic smooth function. The pathological nature of this example is partially illuminated by the fact that its extension to the complex numbers is, in fact, not differentiable.
References
- Glaister, P. (December 1991), A Flat Function with Some Interesting Properties and an Application, The Mathematical Gazette, Vol. 75, No. 474, pp. 438–440
 |