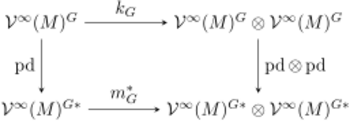Valuation (geometry)
In geometry, a valuation is a finitely additive function from a collection of subsets of a set [math]\displaystyle{ X }[/math] to an abelian semigroup. For example, Lebesgue measure is a valuation on finite unions of convex bodies of [math]\displaystyle{ \R^n. }[/math] Other examples of valuations on finite unions of convex bodies of [math]\displaystyle{ \R^n }[/math] are surface area, mean width, and Euler characteristic.
In geometry, continuity (or smoothness) conditions are often imposed on valuations, but there are also purely discrete facets of the theory. In fact, the concept of valuation has its origin in the dissection theory of polytopes and in particular Hilbert's third problem, which has grown into a rich theory reliant on tools from abstract algebra.
Definition
Let [math]\displaystyle{ X }[/math] be a set, and let [math]\displaystyle{ \mathcal S }[/math] be a collection of subsets of [math]\displaystyle{ X. }[/math] A function [math]\displaystyle{ \phi }[/math] on [math]\displaystyle{ \mathcal S }[/math] with values in an abelian semigroup [math]\displaystyle{ R }[/math] is called a valuation if it satisfies [math]\displaystyle{ \phi(A\cup B)+ \phi(A\cap B) = \phi(A) + \phi(B) }[/math] whenever [math]\displaystyle{ A, }[/math] [math]\displaystyle{ B, }[/math] [math]\displaystyle{ A\cup B, }[/math] and [math]\displaystyle{ A\cap B }[/math] are elements of [math]\displaystyle{ \mathcal S. }[/math] If [math]\displaystyle{ \emptyset\in \mathcal S, }[/math] then one always assumes [math]\displaystyle{ \phi(\emptyset)=0. }[/math]
Examples
Some common examples of [math]\displaystyle{ \mathcal S }[/math] are
- the convex bodies in [math]\displaystyle{ \R^n }[/math]
- compact convex polytopes in [math]\displaystyle{ \R^n }[/math]
- convex cones
- smooth compact polyhedra in a smooth manifold [math]\displaystyle{ X }[/math]
Let [math]\displaystyle{ \mathcal K(\R^n) }[/math] be the set of convex bodies in [math]\displaystyle{ \R^n. }[/math] Then some valuations on [math]\displaystyle{ \mathcal K(\R^n) }[/math] are
- the Euler characteristic [math]\displaystyle{ \chi : K(\R^n) \to \Z }[/math]
- Lebesgue measure restricted to [math]\displaystyle{ \mathcal K(\R^n) }[/math]
- intrinsic volume (and, more generally, mixed volume)
- the map [math]\displaystyle{ A \mapsto h_A, }[/math] where [math]\displaystyle{ h_A }[/math] is the support function of [math]\displaystyle{ A }[/math]
Some other valuations are
- the lattice point enumerator [math]\displaystyle{ P \mapsto |\Z^n\cap P| }[/math], where [math]\displaystyle{ P }[/math] is a lattice polytope
- cardinality, on the family of finite sets
Valuations on convex bodies
From here on, let [math]\displaystyle{ V = \R^n }[/math], let [math]\displaystyle{ \mathcal K(V) }[/math] be the set of convex bodies in [math]\displaystyle{ V }[/math], and let [math]\displaystyle{ \phi }[/math] be a valuation on [math]\displaystyle{ \mathcal K(V) }[/math].
We say [math]\displaystyle{ \phi }[/math] is translation invariant if, for all [math]\displaystyle{ K \in \mathcal K(V) }[/math] and [math]\displaystyle{ x\in V }[/math], we have [math]\displaystyle{ \phi(K+x)=\phi(K) }[/math].
Let [math]\displaystyle{ (K,L) \in \mathcal K(V)^2 }[/math]. The Hausdorff distance [math]\displaystyle{ d_H(K,L) }[/math] is defined as [math]\displaystyle{ d_H(K,L)= \inf\{\varepsilon \gt 0 : K\subset L_\varepsilon \text{ and } L\subset K_\varepsilon \}, }[/math] where [math]\displaystyle{ K_\varepsilon }[/math] is the [math]\displaystyle{ \varepsilon }[/math]-neighborhood of [math]\displaystyle{ K }[/math] under some Euclidean inner product. Equipped with this metric, [math]\displaystyle{ \mathcal K(V) }[/math] is a locally compact space.
The space of continuous, translation-invariant valuations from [math]\displaystyle{ \mathcal K(V) }[/math] to [math]\displaystyle{ \Complex }[/math] is denoted by [math]\displaystyle{ \operatorname{Val}(V). }[/math]
The topology on [math]\displaystyle{ \operatorname{Val}(V) }[/math] is the topology of uniform convergence on compact subsets of [math]\displaystyle{ \mathcal K (V). }[/math] Equipped with the norm [math]\displaystyle{ \|\phi\| = \max\{ |\phi(K)| : K\subset B\}, }[/math] where [math]\displaystyle{ B\subset V }[/math] is a bounded subset with nonempty interior, [math]\displaystyle{ \operatorname{Val}(V) }[/math] is a Banach space.
Homogeneous valuations
A translation-invariant continuous valuation [math]\displaystyle{ \phi\in \operatorname{Val}(V) }[/math] is said to be [math]\displaystyle{ i }[/math]-homogeneous if [math]\displaystyle{ \phi(\lambda K)= \lambda^i\phi(K) }[/math] for all [math]\displaystyle{ \lambda\gt 0 }[/math] and [math]\displaystyle{ K\in \mathcal K(V). }[/math] The subset [math]\displaystyle{ \operatorname{Val}_i(V) }[/math] of [math]\displaystyle{ i }[/math]-homogeneous valuations is a vector subspace of [math]\displaystyle{ \operatorname{Val}(V). }[/math] McMullen's decomposition theorem[1] states that
[math]\displaystyle{ \operatorname{Val}(V)= \bigoplus_{i=0}^n \operatorname{Val}_i(V), \qquad n=\dim V. }[/math]
In particular, the degree of a homogeneous valuation is always an integer between [math]\displaystyle{ 0 }[/math] and [math]\displaystyle{ n=\operatorname{dim} V. }[/math]
Valuations are not only graded by the degree of homogeneity, but also by the parity with respect to the reflection through the origin, namely [math]\displaystyle{ \operatorname{Val}_i = \operatorname{Val}_i^+ \oplus \operatorname{Val}_i^-, }[/math] where [math]\displaystyle{ \phi\in \operatorname{Val}_i^\epsilon }[/math] with [math]\displaystyle{ \epsilon \in \{+,-\} }[/math] if and only if [math]\displaystyle{ \phi(- K)= \epsilon \phi(K) }[/math] for all convex bodies [math]\displaystyle{ K. }[/math] The elements of [math]\displaystyle{ \operatorname{Val}_i^+ }[/math] and [math]\displaystyle{ \operatorname{Val}_i^- }[/math] are said to be even and odd, respectively.
It is a simple fact that [math]\displaystyle{ \operatorname{Val}_0(V) }[/math] is [math]\displaystyle{ 1 }[/math]-dimensional and spanned by the Euler characteristic [math]\displaystyle{ \chi, }[/math] that is, consists of the constant valuations on [math]\displaystyle{ \mathcal K(V). }[/math]
In 1957 Hadwiger[2] proved that [math]\displaystyle{ \operatorname{Val}_n(V) }[/math] (where [math]\displaystyle{ n=\dim V }[/math]) coincides with the [math]\displaystyle{ 1 }[/math]-dimensional space of Lebesgue measures on [math]\displaystyle{ V. }[/math]
A valuation [math]\displaystyle{ \phi\in \operatorname{Val}(\R^n) }[/math] is simple if [math]\displaystyle{ \phi(K)=0 }[/math] for all convex bodies with [math]\displaystyle{ \dim K\lt n. }[/math] Schneider[3] in 1996 described all simple valuations on [math]\displaystyle{ \R^n }[/math]: they are given by [math]\displaystyle{ \phi(K)=c\operatorname{vol}(K)+\int_{S^{n-1}}f(\theta)d\sigma_K(\theta), }[/math] where [math]\displaystyle{ c \in \Complex, }[/math] [math]\displaystyle{ f \in C(S^{n-1}) }[/math] is an arbitrary odd function on the unit sphere [math]\displaystyle{ S^{n-1}\subset \R^n, }[/math] and [math]\displaystyle{ \sigma_K }[/math] is the surface area measure of [math]\displaystyle{ K. }[/math] In particular, any simple valuation is the sum of an [math]\displaystyle{ n }[/math]- and an [math]\displaystyle{ (n-1) }[/math]-homogeneous valuation. This in turn implies that an [math]\displaystyle{ i }[/math]-homogeneous valuation is uniquely determined by its restrictions to all [math]\displaystyle{ (i+1) }[/math]-dimensional subspaces.
Embedding theorems
The Klain embedding is a linear injection of [math]\displaystyle{ \operatorname{Val}_i^+(V), }[/math] the space of even [math]\displaystyle{ i }[/math]-homogeneous valuations, into the space of continuous sections of a canonical complex line bundle over the Grassmannian [math]\displaystyle{ \operatorname{Gr}_i(V) }[/math] of [math]\displaystyle{ i }[/math]-dimensional linear subspaces of [math]\displaystyle{ V. }[/math] Its construction is based on Hadwiger's characterization[2] of [math]\displaystyle{ n }[/math]-homogeneous valuations. If [math]\displaystyle{ \phi\in \operatorname{Val}_i(V) }[/math] and [math]\displaystyle{ E\in \operatorname{Gr}_i(V), }[/math] then the restriction [math]\displaystyle{ \phi|_E }[/math] is an element [math]\displaystyle{ \operatorname{Val}_i(E), }[/math] and by Hadwiger's theorem it is a Lebesgue measure. Hence [math]\displaystyle{ \operatorname{Kl}_\phi(E)= \phi|_E }[/math] defines a continuous section of the line bundle [math]\displaystyle{ Dens }[/math] over [math]\displaystyle{ \operatorname{Gr}_i(V) }[/math] with fiber over [math]\displaystyle{ E }[/math] equal to the [math]\displaystyle{ 1 }[/math]-dimensional space [math]\displaystyle{ \operatorname{Dens}(E) }[/math] of densities (Lebesgue measures) on [math]\displaystyle{ E. }[/math]
Theorem (Klain[4]). The linear map [math]\displaystyle{ \operatorname{Kl} : \operatorname{Val}_i^+(V)\to C(\operatorname{Gr}_i(V),\operatorname{Dens}) }[/math] is injective.
A different injection, known as the Schneider embedding, exists for odd valuations. It is based on Schneider's description of simple valuations.[3] It is a linear injection of [math]\displaystyle{ \operatorname{Val}_i^-(V), }[/math] the space of odd [math]\displaystyle{ i }[/math]-homogeneous valuations, into a certain quotient of the space of continuous sections of a line bundle over the partial flag manifold of cooriented pairs [math]\displaystyle{ (F^i\subset E^{i+1}). }[/math] Its definition is reminiscent of the Klain embedding, but more involved. Details can be found in.[5]
The Goodey-Weil embedding is a linear injection of [math]\displaystyle{ \operatorname{Val}_i }[/math] into the space of distributions on the [math]\displaystyle{ i }[/math]-fold product of the [math]\displaystyle{ (n-1) }[/math]-dimensional sphere. It is nothing but the Schwartz kernel of a natural polarization that any [math]\displaystyle{ \phi\in\operatorname{Val}_k(V) }[/math] admits, namely as a functional on the [math]\displaystyle{ k }[/math]-fold product of [math]\displaystyle{ C^2(S^{n-1}), }[/math] the latter space of functions having the geometric meaning of differences of support functions of smooth convex bodies. For details, see.[5]
Irreducibility Theorem
The classical theorems of Hadwiger, Schneider and McMullen give fairly explicit descriptions of valuations that are homogeneous of degree [math]\displaystyle{ 1, }[/math] [math]\displaystyle{ n-1, }[/math] and [math]\displaystyle{ n=\operatorname{dim} V. }[/math] But for degrees [math]\displaystyle{ 1\lt i\lt n-1 }[/math] very little was known before the turn of the 21st century. McMullen's conjecture is the statement that the valuations [math]\displaystyle{ \phi_A(K)=\operatorname{vol}_n(K+A), \qquad A\in\mathcal K(V), }[/math] span a dense subspace of [math]\displaystyle{ \operatorname{Val}(V). }[/math] McMullen's conjecture was confirmed by Alesker in a much stronger form, which became known as the Irreducibility Theorem:
Theorem (Alesker[6]). For every [math]\displaystyle{ 0\leq i\leq n, }[/math] the natural action of [math]\displaystyle{ GL(V) }[/math] on the spaces [math]\displaystyle{ \operatorname{Val}_i^+(V) }[/math] and [math]\displaystyle{ \operatorname{Val}_i^-(V) }[/math] is irreducible.
Here the action of the general linear group [math]\displaystyle{ GL(V) }[/math] on [math]\displaystyle{ \operatorname{Val}(V) }[/math] is given by [math]\displaystyle{ (g\cdot \phi)(K)= \phi(g^{-1} K). }[/math] The proof of the Irreducibility Theorem is based on the embedding theorems of the previous section and Beilinson-Bernstein localization.
Smooth valuations
A valuation [math]\displaystyle{ \phi\in\operatorname{Val}(V) }[/math] is called smooth if the map [math]\displaystyle{ g\mapsto g\cdot \phi }[/math] from [math]\displaystyle{ GL(V) }[/math] to [math]\displaystyle{ \operatorname{Val}(V) }[/math] is smooth. In other words, [math]\displaystyle{ \phi }[/math] is smooth if and only if [math]\displaystyle{ \phi }[/math] is a smooth vector of the natural representation of [math]\displaystyle{ GL(V) }[/math] on [math]\displaystyle{ \operatorname{Val}(V). }[/math] The space of smooth valuations [math]\displaystyle{ \operatorname{Val}^\infty(V) }[/math] is dense in [math]\displaystyle{ \operatorname{Val}(V) }[/math]; it comes equipped with a natural Fréchet-space topology, which is finer than the one induced from [math]\displaystyle{ \operatorname{Val}(V). }[/math]
For every (complex-valued) smooth function [math]\displaystyle{ f }[/math] on [math]\displaystyle{ \operatorname{Gr}_i(\R^n), }[/math] [math]\displaystyle{ \phi(K)=\int_{\operatorname{Gr}_i(\R^n)} \operatorname{vol}_i(P_E K) f(E) dE, }[/math] where [math]\displaystyle{ P_E : \R^n\to E }[/math] denotes the orthogonal projection and [math]\displaystyle{ dE }[/math] is the Haar measure, defines a smooth even valuation of degree [math]\displaystyle{ i. }[/math] It follows from the Irreducibility Theorem, in combination with the Casselman-Wallach theorem, that any smooth even valuation can be represented in this way. Such a representation is sometimes called a Crofton formula.
For any (complex-valued) smooth differential form [math]\displaystyle{ \omega\in \Omega^{n-1}(\R^n\times S^{n-1}) }[/math] that is invariant under all the translations [math]\displaystyle{ (x,u)\mapsto (x+t,u) }[/math] and every number [math]\displaystyle{ c\in \Complex, }[/math] integration over the normal cycle defines a smooth valuation:
-
[math]\displaystyle{ \phi(K)= c\operatorname{vol}_n(K) + \int_{N(K)} \omega, \qquad K\in \mathcal K(\R^n). }[/math]
()
As a set, the normal cycle [math]\displaystyle{ N(K) }[/math] consists of the outward unit normals to [math]\displaystyle{ K. }[/math] The Irreducibility Theorem implies that every smooth valuation is of this form.
Operations on translation-invariant valuations
There are several natural operations defined on the subspace of smooth valuations [math]\displaystyle{ \operatorname{Val}^\infty(V)\subset \operatorname{Val}(V). }[/math] The most important one is the product of two smooth valuations. Together with pullback and pushforward, this operation extends to valuations on manifolds.
Exterior product
Let [math]\displaystyle{ V,W }[/math] be finite-dimensional real vector spaces. There exists a bilinear map, called the exterior product, [math]\displaystyle{ \boxtimes : \operatorname{Val}^\infty(V)\times \operatorname{Val}^\infty(W)\to \operatorname{Val}(V\times W) }[/math] which is uniquely characterized by the following two properties:
- it is continuous with respect to the usual topologies on [math]\displaystyle{ \operatorname{Val} }[/math] and [math]\displaystyle{ \operatorname{Val}^\infty. }[/math]
- if [math]\displaystyle{ \phi=\operatorname{vol}_V(\bullet + A) }[/math] and [math]\displaystyle{ \psi= \operatorname{vol}_W(\bullet + B) }[/math] where [math]\displaystyle{ A\in \mathcal K(V) }[/math] and [math]\displaystyle{ B\in \mathcal K(W) }[/math] are convex bodies with smooth boundary and strictly positive Gauss curvature, and [math]\displaystyle{ \operatorname{vol}_V }[/math] and [math]\displaystyle{ \operatorname{vol}_W }[/math] are densities on [math]\displaystyle{ V }[/math] and [math]\displaystyle{ W, }[/math] then
[math]\displaystyle{ \phi\boxtimes \psi = (\operatorname{vol}_V\boxtimes \operatorname{vol}_W) (\bullet + A\times B). }[/math]
Product
The product of two smooth valuations [math]\displaystyle{ \phi,\psi\in\operatorname{Val}^\infty (V) }[/math] is defined by [math]\displaystyle{ (\phi\cdot \psi)(K)= (\phi\boxtimes \psi)(\Delta(K)), }[/math] where [math]\displaystyle{ \Delta : V\to V\times V }[/math] is the diagonal embedding. The product is a continuous map [math]\displaystyle{ \operatorname{Val}^\infty (V) \times \operatorname{Val}^\infty (V) \to \operatorname{Val}^\infty (V) . }[/math] Equipped with this product, [math]\displaystyle{ \operatorname{Val}^\infty (V) }[/math] becomes a commutative associative graded algebra with the Euler characteristic as the multiplicative identity.
Alesker-Poincaré duality
By a theorem of Alesker, the restriction of the product [math]\displaystyle{ \operatorname{Val}_k^\infty(V)\times \operatorname{Val}_{n-k}^\infty(V)\to \operatorname{Val}_n^\infty(V)=\operatorname{Dens}(V) }[/math] is a non-degenerate pairing. This motivates the definition of the [math]\displaystyle{ k }[/math]-homogeneous generalized valuation, denoted [math]\displaystyle{ \operatorname{Val}_k^{-\infty}(V), }[/math] as [math]\displaystyle{ \operatorname{Val}^\infty_{n-k}(V)^*\otimes\operatorname{Dens}(V), }[/math] topologized with the weak topology. By the Alesker-Poincaré duality, there is a natural dense inclusion [math]\displaystyle{ \operatorname{Val}_k^\infty(V)\hookrightarrow\operatorname{Val}_k^{-\infty}(V)/ }[/math]
Convolution
Convolution is a natural product on [math]\displaystyle{ \operatorname{Val}^\infty(V)\otimes \operatorname{Dens}(V^*). }[/math] For simplicity, we fix a density [math]\displaystyle{ \operatorname{vol} }[/math] on [math]\displaystyle{ V }[/math] to trivialize the second factor. Define for fixed [math]\displaystyle{ A,B\in\mathcal K(V) }[/math] with smooth boundary and strictly positive Gauss curvature [math]\displaystyle{ \operatorname{vol}(\bullet+A)\ast\operatorname{vol}(\bullet+B)=\operatorname{vol}(\bullet+A+B). }[/math] There is then a unique extension by continuity to a map [math]\displaystyle{ \operatorname{Val}^\infty (V) \times \operatorname{Val}^\infty (V) \to \operatorname{Val}^\infty (V), }[/math] called the convolution. Unlike the product, convolution respects the co-grading, namely if [math]\displaystyle{ \phi\in\operatorname{Val}^\infty_{n-i}(V), }[/math] [math]\displaystyle{ \psi\in\operatorname{Val}^\infty_{n-j}(V), }[/math] then [math]\displaystyle{ \phi\ast\psi\in \operatorname{Val}^\infty_{n-i-j}(V). }[/math]
For instance, let [math]\displaystyle{ V(K_1,\ldots, K_n) }[/math] denote the mixed volume of the convex bodies [math]\displaystyle{ K_1,\ldots, K_n\subset \R^n. }[/math] If convex bodies [math]\displaystyle{ A_1,\dots,A_{n-i} }[/math] in [math]\displaystyle{ \R^n }[/math] with a smooth boundary and strictly positive Gauss curvature are fixed, then [math]\displaystyle{ \phi(K) = V(K[i], A_1,\dots,A_{n-i}) }[/math] defines a smooth valuation of degree [math]\displaystyle{ i. }[/math] The convolution two such valuations is [math]\displaystyle{ V(\bullet[i], A_1,\dots,A_{n-i})\ast V(\bullet[j],B_1,\dots,B_{n-j})=c_{i,j}V(\bullet[n-j-i], A_1,\dots,A_{n-i},B_1,\dots,B_{n-j}), }[/math] where [math]\displaystyle{ c_{i,j} }[/math] is a constant depending only on [math]\displaystyle{ i,j,n. }[/math]
Fourier transform
The Alesker-Fourier transform is a natural, [math]\displaystyle{ GL(V) }[/math]-equivariant isomorphism of complex-valued valuations [math]\displaystyle{ \mathbb F: \operatorname{Val}^\infty(V)\to \operatorname{Val}^\infty(V^*)\otimes \operatorname{Dens}(V), }[/math] discovered by Alesker and enjoying many properties resembling the classical Fourier transform, which explains its name.
It reverses the grading, namely [math]\displaystyle{ \mathbb F: \operatorname{Val}_k^\infty(V) \to \operatorname{Val}^\infty_{n-k}(V^*)\otimes \operatorname{Dens}(V), }[/math] and intertwines the product and the convolution: [math]\displaystyle{ \mathbb F(\phi\cdot \psi) = \mathbb F\phi\ast\mathbb F\psi. }[/math]
Fixing for simplicity a Euclidean structure to identify [math]\displaystyle{ V = V^*, }[/math] [math]\displaystyle{ \operatorname{Dens}(V)=\Complex, }[/math] we have the identity [math]\displaystyle{ \mathbb F^2\phi(K) = \phi(-K). }[/math] On even valuations, there is a simple description of the Fourier transform in terms of the Klain embedding: [math]\displaystyle{ \operatorname{Kl}_{\mathbb F\phi}(E) = \operatorname{Kl}_\phi(E^\perp). }[/math] In particular, even real-valued valuations remain real-valued after the Fourier transform.
For odd valuations, the description of the Fourier transform is substantially more involved. Unlike the even case, it is no longer of purely geometric nature. For instance, the space of real-valued odd valuations is not preserved.
Pullback and pushforward
Given a linear map [math]\displaystyle{ f:U\to V, }[/math] there are induced operations of pullback [math]\displaystyle{ f^*:\operatorname{Val}(V)\to \operatorname{Val}(U) }[/math] and pushforward [math]\displaystyle{ f_*:\operatorname{Val}(U)\otimes\operatorname{Dens}(U)^*\to \operatorname{Val}(V)\otimes \operatorname{Dens}(V)^*. }[/math] The pullback is the simpler of the two, given by [math]\displaystyle{ f^*\phi(K)=\phi(f(K)). }[/math] It evidently preserves the parity and degree of homogeneity of a valuation. Note that the pullback does not preserve smoothness when [math]\displaystyle{ f }[/math] is not injective.
The pushforward is harder to define formally. For simplicity, fix Lebesgue measures on [math]\displaystyle{ U }[/math] and [math]\displaystyle{ V. }[/math] The pushforward can be uniquely characterized by describing its action on valuations of the form [math]\displaystyle{ \operatorname{vol}(\bullet+A), }[/math] for all [math]\displaystyle{ A\in \mathcal K(U), }[/math] and then extended by continuity to all valuations using the Irreducibility Theorem. For a surjective map [math]\displaystyle{ f, }[/math] [math]\displaystyle{ f_*\operatorname{vol}(\bullet+A)=\operatorname{vol}(\bullet+f(A)). }[/math] For an inclusion [math]\displaystyle{ f:U\hookrightarrow V, }[/math] choose a splitting [math]\displaystyle{ V=U\oplus W. }[/math] Then [math]\displaystyle{ f_*\operatorname{vol}(\bullet + A) (K)= \int_{W}\operatorname{vol}(K\cap (U+w) + A) dw. }[/math] Informally, the pushforward is dual to the pullback with respect to the Alesker-Poincaré pairing: for [math]\displaystyle{ \phi\in \operatorname{Val}(V) }[/math] and [math]\displaystyle{ \psi\in\operatorname{Val}(U)\otimes\operatorname{Dens}(U)^*, }[/math] [math]\displaystyle{ \langle f^*\phi,\psi\rangle =\langle \phi, f_*\psi\rangle. }[/math] However, this identity has to be carefully interpreted since the pairing is only well-defined for smooth valuations. For further details, see.[7]
Valuations on manifolds
In a series of papers beginning in 2006, Alesker laid down the foundations for a theory of valuations on manifolds that extends the theory of valuations on convex bodies. The key observation leading to this extension is that via integration over the normal cycle (1), a smooth translation-invariant valuation may be evaluated on sets much more general than convex ones. Also (1) suggests to define smooth valuations in general by dropping the requirement that the form [math]\displaystyle{ \omega }[/math] be translation-invariant and by replacing the translation-invariant Lebesgue measure with an arbitrary smooth measure.
Let [math]\displaystyle{ X }[/math] be an n-dimensional smooth manifold and let [math]\displaystyle{ \mathbb P_X= \mathbb P_+(T^* X) }[/math] be the co-sphere bundle of [math]\displaystyle{ X, }[/math] that is, the oriented projectivization of the cotangent bundle. Let [math]\displaystyle{ \mathcal P(X) }[/math] denote the collection of compact differentiable polyhedra in [math]\displaystyle{ X. }[/math] The normal cycle [math]\displaystyle{ N(A)\subset \mathbb P_X }[/math] of [math]\displaystyle{ A\in \mathcal P(X), }[/math] which consists of the outward co-normals to [math]\displaystyle{ A, }[/math] is naturally a Lipschitz submanifold of dimension [math]\displaystyle{ n-1. }[/math]
For ease of presentation we henceforth assume that [math]\displaystyle{ X }[/math] is oriented, even though the concept of smooth valuations in fact does not depend on orientability. The space of smooth valuations [math]\displaystyle{ \mathcal V^\infty(X) }[/math] on [math]\displaystyle{ X }[/math] consists of functions [math]\displaystyle{ \phi : \mathcal P(X)\to \Complex }[/math] of the form [math]\displaystyle{ \phi(A)= \int_A\mu + \int_{N(A)}\omega,\qquad A\in \mathcal P(X), }[/math] where [math]\displaystyle{ \mu\in\Omega^n(X) }[/math] and [math]\displaystyle{ \omega\in \Omega^{n-1}(\mathbb P_X) }[/math] can be arbitrary. It was shown by Alesker that the smooth valuations on open subsets of [math]\displaystyle{ X }[/math] form a soft sheaf over [math]\displaystyle{ X. }[/math]
Examples
The following are examples of smooth valuations on a smooth manifold [math]\displaystyle{ X }[/math]:
- Smooth measures on [math]\displaystyle{ X. }[/math]
- The Euler characteristic; this follows from the work of Chern[8] on the Gauss-Bonnet theorem, where such [math]\displaystyle{ \mu }[/math] and [math]\displaystyle{ \omega }[/math] were constructed to represent the Euler characteristic. In particular, [math]\displaystyle{ \mu }[/math] is then the Chern-Gauss-Bonnet integrand, which is the Pfaffian of the Riemannian curvature tensor.
- If [math]\displaystyle{ X }[/math] is Riemannian, then the Lipschitz-Killing valuations or intrinsic volumes [math]\displaystyle{ V_0^X = \chi, V_1^X, \ldots, V_n^X = \mathrm{vol}_X }[/math] are smooth valuations. If [math]\displaystyle{ f : X \to \R^m }[/math] is any isometric immersion into a Euclidean space, then [math]\displaystyle{ V_i^X = f^* V_i^{\R^m}, }[/math] where [math]\displaystyle{ V_i^{\R^m} }[/math] denotes the usual intrinsic volumes on [math]\displaystyle{ \R^m }[/math] (see below for the definition of the pullback). The existence of these valuations is the essence of Weyl's tube formula.[9]
- Let [math]\displaystyle{ \Complex P^n }[/math] be the complex projective space, and let [math]\displaystyle{ \mathrm{Gr}_k^\Complex }[/math] denote the Grassmannian of all complex projective subspaces of fixed dimension [math]\displaystyle{ k. }[/math] The function
[math]\displaystyle{ \phi(A) = \int_{\mathrm{Gr}_k^\Complex} \chi(A\cap E) dE, \qquad A\in \mathcal P (\Complex P^n), }[/math] where the integration is with respect to the Haar probability measure on [math]\displaystyle{ \mathrm{Gr}_k^\Complex, }[/math] is a smooth valuation. This follows from the work of Fu.[10]
Filtration
The space [math]\displaystyle{ \mathcal V^\infty(X) }[/math] admits no natural grading in general, however it carries a canonical filtration [math]\displaystyle{ \mathcal V^\infty(X) = W_0\supset W_1\supset \cdots \supset W_n. }[/math] Here [math]\displaystyle{ W_n }[/math] consists of the smooth measures on [math]\displaystyle{ X, }[/math] and [math]\displaystyle{ W_j }[/math] is given by forms [math]\displaystyle{ \omega }[/math] in the ideal generated by [math]\displaystyle{ \pi^*\Omega^j(X), }[/math] where [math]\displaystyle{ \pi : \mathbb P_X\to X }[/math] is the canonical projection.
The associated graded vector space [math]\displaystyle{ \bigoplus_{i=0}^n W_i/W_{i+1} }[/math] is canonically isomorphic to the space of smooth sections [math]\displaystyle{ \bigoplus_{i=0}^n C^\infty (X, \operatorname{Val}_i^\infty(TX)), }[/math] where [math]\displaystyle{ \operatorname{Val}_i^\infty(TX) }[/math] denotes the vector bundle over [math]\displaystyle{ X }[/math] such that the fiber over a point [math]\displaystyle{ x\in X }[/math] is [math]\displaystyle{ \operatorname{Val}_i^\infty(T_x X), }[/math] the space of [math]\displaystyle{ i }[/math]-homogeneous smooth translation-invariant valuations on the tangent space [math]\displaystyle{ T_x X. }[/math]
Product
The space [math]\displaystyle{ \mathcal V^\infty(X) }[/math] admits a natural product. This product is continuous, commutative, associative, compatible with the filtration: [math]\displaystyle{ W_i\cdot W_j\subset W_{i+j}, }[/math] and has the Euler characteristic as the identity element. It also commutes with the restriction to embedded submanifolds, and the diffeomorphism group of [math]\displaystyle{ X }[/math] acts on [math]\displaystyle{ \mathcal V^\infty(X) }[/math] by algebra automorphisms.
For example, if [math]\displaystyle{ X }[/math] is Riemannian, the Lipschitz-Killing valuations satisfy [math]\displaystyle{ V_i^X\cdot V_j^X= V_{i+j}^X. }[/math]
The Alesker-Poincaré duality still holds. For compact [math]\displaystyle{ X }[/math] it says that the pairing [math]\displaystyle{ \mathcal V^\infty(X)\times \mathcal V^\infty(X)\to \Complex, }[/math] [math]\displaystyle{ (\phi, \psi)\mapsto (\phi\cdot\psi) (X) }[/math] is non-degenerate. As in the translation-invariant case, this duality can be used to define generalized valuations. Unlike the translation-invariant case, no good definition of continuous valuations exists for valuations on manifolds.
The product of valuations closely reflects the geometric operation of intersection of subsets. Informally, consider the generalized valuation [math]\displaystyle{ \chi_A=\chi(A\cap\bullet). }[/math] The product is given by [math]\displaystyle{ \chi_A\cdot\chi_B=\chi_{A\cap B}. }[/math] Now one can obtain smooth valuations by averaging generalized valuations of the form [math]\displaystyle{ \chi_A, }[/math] more precisely [math]\displaystyle{ \phi(X)=\int_S \chi_{s(A)}ds }[/math] is a smooth valuation if [math]\displaystyle{ S }[/math] is a sufficiently large measured family of diffeomorphisms. Then one has [math]\displaystyle{ \int_S \chi_{s(A)}ds\cdot \int_{S'} \chi_{s'(B)}ds'=\int_{S\times S'} \chi_{s(A)\cap s'(B)}dsds', }[/math] see.[11]
Pullback and pushforward
Every smooth immersion [math]\displaystyle{ f : X \to Y }[/math] of smooth manifolds induces a pullback map [math]\displaystyle{ f^* : \mathcal V^\infty(Y) \to \mathcal V^\infty(X). }[/math] If [math]\displaystyle{ f }[/math] is an embedding, then [math]\displaystyle{ (f^* \phi)(A) = \phi(f(A)), \qquad A\in\mathcal P (X). }[/math] The pullback is a morphism of filtered algebras. Every smooth proper submersion [math]\displaystyle{ f : X\to Y }[/math] defines a pushforward map [math]\displaystyle{ f^* : \mathcal V^\infty(X) \to \mathcal V^\infty(Y) }[/math] by [math]\displaystyle{ (f_* \phi)(A) = \phi(f^{-1}(A)), \qquad A\in\mathcal P (Y). }[/math] The pushforward is compatible with the filtration as well: [math]\displaystyle{ f_* : W_i(X)\to W_{i-(\dim X-\dim Y)}(Y). }[/math] For general smooth maps, one can define pullback and pushforward for generalized valuations under some restrictions.
Applications in Integral Geometry
Let [math]\displaystyle{ M }[/math] be a Riemannian manifold and let [math]\displaystyle{ G }[/math] be a Lie group of isometries of [math]\displaystyle{ M }[/math] acting transitively on the sphere bundle [math]\displaystyle{ SM. }[/math] Under these assumptions the space [math]\displaystyle{ \mathcal V^\infty(M)^G }[/math] of [math]\displaystyle{ G }[/math]-invariant smooth valuations on [math]\displaystyle{ M }[/math] is finite-dimensional; let [math]\displaystyle{ \phi_1, \ldots, \phi_m }[/math] be a basis. Let [math]\displaystyle{ A,B\in \mathcal P(M) }[/math] be differentiable polyhedra in [math]\displaystyle{ M. }[/math] Then integrals of the form [math]\displaystyle{ \int_G \phi_i(A\cap gB)dg }[/math] are expressible as linear combinations of [math]\displaystyle{ \phi_k(A)\phi_l(B) }[/math] with coefficients [math]\displaystyle{ c_i^{kl} }[/math] independent of [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math]:
-
[math]\displaystyle{ \int_G \phi_i(A\cap gB)dg = \sum_{k,l=1}^m c_i^{kl} \phi_k(A)\phi_l(B),\qquad A,B \in \mathcal P(M). }[/math]
()
Formulas of this type are called kinematic formulas. Their existence in this generality was proved by Fu.[10] For the three simply connected real space forms, that is, the sphere, Euclidean space, and hyperbolic space, they go back to Blaschke, Santaló, Chern, and Federer.
Describing the kinematic formulas explicitly is typically a difficult problem. In fact already in the step from real to complex space forms, considerable difficulties arise and these have only recently been resolved by Bernig, Fu, and Solanes.[12] [13] The key insight responsible for this progress is that the kinematic formulas contain the same information as the algebra of invariant valuations [math]\displaystyle{ \mathcal V^\infty(M)^G. }[/math] For a precise statement, let [math]\displaystyle{ k_G : \mathcal V^\infty(M)^G \to \mathcal V^\infty(M)^G\otimes \mathcal V^\infty(M)^G }[/math] be the kinematic operator, that is, the map determined by the kinematic formulas (2). Let [math]\displaystyle{ \operatorname{pd} : \mathcal V^\infty(M)^G \to \mathcal V^\infty(M)^{G*} }[/math] denote the Alesker-Poincaré duality, which is a linear isomorphism. Finally let [math]\displaystyle{ m_G^* }[/math] be the adjoint of the product map [math]\displaystyle{ m_G : \mathcal V^\infty(M)^{G}\otimes \mathcal V^\infty(M)^{G} \to \mathcal V^\infty(M)^{G}. }[/math] The Fundamental theorem of algebraic integral geometry relating operations on valuations to integral geometry, states that if the Poincaré duality is used to identify [math]\displaystyle{ \mathcal V^\infty(M)^{G} }[/math] with [math]\displaystyle{ \mathcal V^\infty(M)^{G*}, }[/math] then [math]\displaystyle{ k_G=m_G^* }[/math]:
See also
- Hadwiger's theorem
- Integral geometry
- Mixed volume
- Set function – Function from sets to numbers
- Valuation (measure theory)
References
- ↑ "Continuous translation-invariant valuations on the space of compact convex sets", Archiv der Mathematik 34 (4): 377–384, 1980, doi:10.1007/BF01224974
- ↑ 2.0 2.1 Vorlesungen über Inhalt, Oberfläche und Isoperimetrie, Die Grundlehren der Mathematischen Wissenschaften, 93, Berlin-Göttingen-Heidelberg: Springer-Verlag, 1957, doi:10.1007/978-3-642-94702-5, ISBN 978-3-642-94703-2
- ↑ 3.0 3.1 Schneider, Rolf (1996), "Simple valuations on convex bodies", Mathematika 43 (1): 32–39, doi:10.1112/S0025579300011578
- ↑ Klain, Daniel A. (1995), "A short proof of Hadwiger's characterization theorem", Mathematika 42 (2): 329–339, doi:10.1112/S0025579300014625
- ↑ 5.0 5.1 Alesker, Semyon (2018), Introduction to the theory of valuations, CBMS Regional Conference Series in Mathematics, 126, Providence, RI: American Mathematical Society
- ↑ Alesker, Semyon (2001), "Description of translation invariant valuations on convex sets with solution of P. McMullen's conjecture", Geometric and Functional Analysis 11 (2): 244–272, doi:10.1007/PL00001675
- ↑ Alesker, Semyon (2011), "A Fourier-type transform on translation-invariant valuations on convex sets", Israel Journal of Mathematics 181: 189–294, doi:10.1007/s11856-011-0008-6
- ↑ "On the curvatura integra in a Riemannian manifold", Annals of Mathematics, Second Series 46 (4): 674–684, 1945, doi:10.2307/1969203
- ↑ Weyl, Hermann (1939), "On the Volume of Tubes", American Journal of Mathematics 61 (2): 461–472, doi:10.2307/2371513
- ↑ 10.0 10.1 Fu, Joseph H. G. (1990), "Kinematic formulas in integral geometry", Indiana University Mathematics Journal 39 (4): 1115–1154, doi:10.1512/iumj.1990.39.39052
- ↑ Fu, Joseph H. G. (2016), "Intersection theory and the Alesker product", Indiana University Mathematics Journal 65 (4): 1347–1371, doi:10.1512/iumj.2016.65.5846
- ↑ Bernig, Andreas; Fu, Joseph H. G.; Solanes, Gil (2014), "Integral geometry of complex space forms", Geometric and Functional Analysis 24 (2): 403–49, doi:10.1007/s00039-014-0251-12
- ↑ Bernig, Andreas; Fu, Joseph H. G. (2011), "Hermitian integral geometry", Annals of Mathematics, Second Series 173 (2): 907–945, doi:10.4007/annals.2011.173.2.7
Bibliography
- S. Alesker (2018). Introduction to the theory of valuations. CBMS Regional Conference Series in Mathematics, 126. American Mathematical Society, Providence, RI. ISBN 978-1-4704-4359-7.
- S. Alesker; J. H. G. Fu (2014). Integral geometry and valuations. Advanced Courses in Mathematics. CRM Barcelona.. Birkhäuser/Springer, Basel. ISBN 978-1-4704-4359-7.
- D. A. Klain; G.-C. Rota (1997). Introduction to geometric probability. Lezioni Lincee. [Lincei Lectures]. Cambridge University Press. ISBN 0-521-59362-X.
- R. Schneider (2014). Convex bodies: the Brunn-Minkowski theory.. Encyclopedia of Mathematics and its Applications, 151.. Cambridge University Press, Cambridge, RI. ISBN 978-1-107-60101-7.
 |