Tournament (graph theory)
| Tournament | |
|---|---|
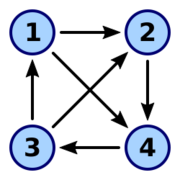 A tournament on 4 vertices | |
| Vertices | [math]\displaystyle{ n }[/math] |
| Edges | [math]\displaystyle{ \binom{n}{2} }[/math] |
| Table of graphs and parameters | |
A tournament is a directed graph (digraph) obtained by assigning a direction for each edge in an undirected complete graph. That is, it is an orientation of a complete graph, or equivalently a directed graph in which every pair of distinct vertices is connected by a directed edge (often, called an arc) with any one of the two possible orientations.
Many of the important properties of tournaments were first investigated by H. G. Landau in (Landau 1953) to model dominance relations in flocks of chickens. Current applications of tournaments include the study of voting theory and social choice theory among other things.
The name tournament originates from such a graph's interpretation as the outcome of a round-robin tournament in which every player encounters every other player exactly once, and in which no draws occur. In the tournament digraph, the vertices correspond to the players. The edge between each pair of players is oriented from the winner to the loser. If player [math]\displaystyle{ a }[/math] beats player [math]\displaystyle{ b }[/math], then it is said that [math]\displaystyle{ a }[/math] dominates [math]\displaystyle{ b }[/math]. If every player beats the same number of other players (indegree = outdegree), the tournament is called regular.
Paths and cycles
Theorem — Any tournament on a finite number [math]\displaystyle{ n }[/math] of vertices contains a Hamiltonian path, i.e., directed path on all [math]\displaystyle{ n }[/math] vertices (Rédei 1934).
This is easily shown by induction on [math]\displaystyle{ n }[/math]: suppose that the statement holds for [math]\displaystyle{ n }[/math], and consider any tournament [math]\displaystyle{ T }[/math] on [math]\displaystyle{ n+1 }[/math] vertices. Choose a vertex [math]\displaystyle{ v_0 }[/math] of [math]\displaystyle{ T }[/math] and consider a directed path [math]\displaystyle{ v_1,v_2,\ldots,v_n }[/math] in [math]\displaystyle{ T\setminus \{v_0\} }[/math]. There is some [math]\displaystyle{ i \in \{0,\ldots,n\} }[/math] such that [math]\displaystyle{ (i=0 \vee v_i \rightarrow v_0) \wedge (v_0 \rightarrow v_{i+1} \vee i=n) }[/math]. (One possibility is to let [math]\displaystyle{ i \in \{0,\ldots,n\} }[/math] be maximal such that for every [math]\displaystyle{ j \leq i, v_j \rightarrow v_0 }[/math]. Alternatively, let [math]\displaystyle{ i }[/math] be minimal such that [math]\displaystyle{ \forall j \gt i, v_0 \rightarrow v_j }[/math].)
- [math]\displaystyle{ v_1,\ldots,v_i,v_0,v_{i+1},\ldots,v_n }[/math]
is a directed path as desired. This argument also gives an algorithm for finding the Hamiltonian path. More efficient algorithms, that require examining only [math]\displaystyle{ O(n \log n) }[/math] of the edges, are known. The Hamiltonian paths are in one-to-one correspondence with the minimal feedback arc sets of the tournament.[1] Rédei's theorem is the special case for complete graphs of the Gallai–Hasse–Roy–Vitaver theorem, relating the lengths of paths in orientations of graphs to the chromatic number of these graphs.[2]
Another basic result on tournaments is that every strongly connected tournament has a Hamiltonian cycle.[3] More strongly, every strongly connected tournament is vertex pancyclic: for each vertex [math]\displaystyle{ v }[/math], and each [math]\displaystyle{ k }[/math] in the range from three to the number of vertices in the tournament, there is a cycle of length [math]\displaystyle{ k }[/math] containing [math]\displaystyle{ v }[/math].[4] A tournament [math]\displaystyle{ T }[/math]is [math]\displaystyle{ k }[/math]-strongly connected if for every set [math]\displaystyle{ U }[/math] of [math]\displaystyle{ k-1 }[/math] vertices of [math]\displaystyle{ T }[/math], [math]\displaystyle{ T-U }[/math] is strongly connected. If the tournament is 4‑strongly connected, then each pair of vertices can be connected with a Hamiltonian path.[5] For every set [math]\displaystyle{ B }[/math] of at most [math]\displaystyle{ k-1 }[/math] arcs of a [math]\displaystyle{ k }[/math]-strongly connected tournament [math]\displaystyle{ T }[/math], we have that [math]\displaystyle{ T-B }[/math] has a Hamiltonian cycle.[6] This result was extended by (Bang-Jensen Gutin).
Transitivity
A tournament in which [math]\displaystyle{ ((a \rightarrow b) }[/math] and [math]\displaystyle{ (b \rightarrow c)) }[/math] [math]\displaystyle{ \Rightarrow }[/math] [math]\displaystyle{ (a \rightarrow c) }[/math] is called transitive. In other words, in a transitive tournament, the vertices may be (strictly) totally ordered by the edge relation, and the edge relation is the same as reachability.
Equivalent conditions
The following statements are equivalent for a tournament [math]\displaystyle{ T }[/math] on [math]\displaystyle{ n }[/math] vertices:
- [math]\displaystyle{ T }[/math] is transitive.
- [math]\displaystyle{ T }[/math] is a strict total ordering.
- [math]\displaystyle{ T }[/math] is acyclic.
- [math]\displaystyle{ T }[/math] does not contain a cycle of length 3.
- The score sequence (set of outdegrees) of [math]\displaystyle{ T }[/math] is [math]\displaystyle{ \{0,1,2,\ldots,n-1\} }[/math].
- [math]\displaystyle{ T }[/math] has exactly one Hamiltonian path.
Ramsey theory
Transitive tournaments play a role in Ramsey theory analogous to that of cliques in undirected graphs. In particular, every tournament on [math]\displaystyle{ n }[/math] vertices contains a transitive subtournament on [math]\displaystyle{ 1+\lfloor\log_2 n\rfloor }[/math] vertices.[7] The proof is simple: choose any one vertex [math]\displaystyle{ v }[/math] to be part of this subtournament, and form the rest of the subtournament recursively on either the set of incoming neighbors of [math]\displaystyle{ v }[/math] or the set of outgoing neighbors of [math]\displaystyle{ v }[/math], whichever is larger. For instance, every tournament on seven vertices contains a three-vertex transitive subtournament; the Paley tournament on seven vertices shows that this is the most that can be guaranteed (Erdős Moser). However, (Reid Parker) showed that this bound is not tight for some larger values of [math]\displaystyle{ n }[/math].
(Erdős Moser) proved that there are tournaments on [math]\displaystyle{ n }[/math] vertices without a transitive subtournament of size [math]\displaystyle{ 2+2\lfloor\log_2 n\rfloor }[/math] Their proof uses a counting argument: the number of ways that a [math]\displaystyle{ k }[/math]-element transitive tournament can occur as a subtournament of a larger tournament on [math]\displaystyle{ n }[/math] labeled vertices is
- [math]\displaystyle{ \binom{n}{k}k!2^{\binom{n}{2}-\binom{k}{2}}, }[/math]
and when [math]\displaystyle{ k }[/math] is larger than [math]\displaystyle{ 2+2\lfloor\log_2 n\rfloor }[/math], this number is too small to allow for an occurrence of a transitive tournament within each of the [math]\displaystyle{ 2^{\binom{n}{2}} }[/math] different tournaments on the same set of [math]\displaystyle{ n }[/math] labeled vertices.
Paradoxical tournaments
A player who wins all games would naturally be the tournament's winner. However, as the existence of non-transitive tournaments shows, there may not be such a player. A tournament for which every player loses at least one game is called a 1-paradoxical tournament. More generally, a tournament [math]\displaystyle{ T=(V,E) }[/math] is called [math]\displaystyle{ k }[/math]-paradoxical if for every [math]\displaystyle{ k }[/math]-element subset [math]\displaystyle{ S }[/math] of [math]\displaystyle{ V }[/math] there is a vertex [math]\displaystyle{ v_0 }[/math] in [math]\displaystyle{ V\setminus S }[/math] such that [math]\displaystyle{ v_0 \rightarrow v }[/math] for all [math]\displaystyle{ v \in S }[/math]. By means of the probabilistic method, Paul Erdős showed that for any fixed value of [math]\displaystyle{ k }[/math], if [math]\displaystyle{ |V| \geq k^22^k\ln(2+o(1)) }[/math], then almost every tournament on [math]\displaystyle{ V }[/math] is [math]\displaystyle{ k }[/math]-paradoxical.[8] On the other hand, an easy argument shows that any [math]\displaystyle{ k }[/math]-paradoxical tournament must have at least [math]\displaystyle{ 2^{k+1}-1 }[/math] players, which was improved to [math]\displaystyle{ (k+2)2^{k-1}-1 }[/math] by Esther and George Szekeres (1965).[9] There is an explicit construction of [math]\displaystyle{ k }[/math]-paradoxical tournaments with [math]\displaystyle{ k^24^{k-1}(1+o(1)) }[/math] players by Graham and Spencer (1971) namely the Paley tournament.
Condensation
The condensation of any tournament is itself a transitive tournament. Thus, even for tournaments that are not transitive, the strongly connected components of the tournament may be totally ordered.[10]
Score sequences and score sets
The score sequence of a tournament is the nondecreasing sequence of outdegrees of the vertices of a tournament. The score set of a tournament is the set of integers that are the outdegrees of vertices in that tournament.
Landau's Theorem (1953) A nondecreasing sequence of integers [math]\displaystyle{ (s_1, s_2, \ldots, s_n) }[/math] is a score sequence if and only if :
- [math]\displaystyle{ 0 \le s_1 \le s_2 \le \cdots \le s_n }[/math]
- [math]\displaystyle{ s_1 + s_2 + \cdots + s_i \ge {i \choose 2}, \text{ for }i = 1, 2, \ldots, n - 1 }[/math]
- [math]\displaystyle{ s_1 + s_2 + \cdots + s_n = {n \choose 2}. }[/math]
Let [math]\displaystyle{ s(n) }[/math] be the number of different score sequences of size [math]\displaystyle{ n }[/math]. The sequence [math]\displaystyle{ s(n) }[/math] (sequence A000571 in the OEIS) starts as:
1, 1, 1, 2, 4, 9, 22, 59, 167, 490, 1486, 4639, 14805, 48107, ...
Winston and Kleitman proved that for sufficiently large n:
- [math]\displaystyle{ s(n) \gt c_1 4^n n^{-5/2}, }[/math]
where [math]\displaystyle{ c_1 = 0.049. }[/math] Takács later showed, using some reasonable but unproven assumptions, that
- [math]\displaystyle{ s(n) \lt c_2 4^n n^{-5/2}, }[/math]
where [math]\displaystyle{ c_2 \lt 4.858. }[/math]
Together these provide evidence that:
- [math]\displaystyle{ s(n) \in \Theta (4^n n^{-5/2}). }[/math]
Here [math]\displaystyle{ \Theta }[/math] signifies an asymptotically tight bound.
Yao showed that every nonempty set of nonnegative integers is the score set for some tournament.
Majority relations
In social choice theory, tournaments naturally arise as majority relations of preference profiles.[11] Let [math]\displaystyle{ A }[/math] be a finite set of alternatives, and consider a list [math]\displaystyle{ P = (\succ_1, \dots, \succ_n) }[/math] of linear orders over [math]\displaystyle{ A }[/math]. We interpret each order [math]\displaystyle{ \succ_i }[/math] as the preference ranking of a voter [math]\displaystyle{ i }[/math]. The (strict) majority relation [math]\displaystyle{ \succ_{\text{maj}} }[/math] of [math]\displaystyle{ P }[/math] over [math]\displaystyle{ A }[/math] is then defined so that [math]\displaystyle{ a \succ_{\text{maj}} b }[/math] if and only if a majority of the voters prefer [math]\displaystyle{ a }[/math] to [math]\displaystyle{ b }[/math], that is [math]\displaystyle{ |\{ i \in [n] : a \succ_i b \}| \gt |\{ i \in [n] : b \succ_i a \}| }[/math]. If the number [math]\displaystyle{ n }[/math] of voters is odd, then the majority relation forms the dominance relation of a tournament on vertex set [math]\displaystyle{ A }[/math].
By a lemma of McGarvey, every tournament on [math]\displaystyle{ m }[/math] vertices can be obtained as the majority relation of at most [math]\displaystyle{ m(m-1) }[/math] voters.[11][12] Results by Stearns and Erdős & Moser later established that [math]\displaystyle{ \Theta(m/\log m) }[/math] voters are needed to induce every tournament on [math]\displaystyle{ m }[/math] vertices.[13]
Laslier (1997) studies in what sense a set of vertices can be called the set of "winners" of a tournament. This revealed to be useful in Political Science to study, in formal models of political economy, what can be the outcome of a democratic process.[14]
See also
- Oriented graph
- Paley tournament
- Sumner's conjecture
- Tournament solution
Notes
- ↑ Bar-Noy & Naor (1990).
- ↑ Havet (2013).
- ↑ Camion (1959).
- ↑ Moon (1966), Theorem 1.
- ↑ Thomassen (1980).
- ↑ Fraisse & Thomassen (1987).
- ↑ (Erdős Moser).
- ↑ (Erdős 1963)
- ↑ Szekeres, E.; Szekeres, G. (1965). "On a problem of Schütte and Erdős". Math. Gaz. 49: 290–293.
- ↑ (Harary Moser), Corollary 5b.
- ↑ 11.0 11.1 Brandt, Felix and Brill, Markus and Harrenstein, Paul, "Tournament Solutions". Chapter 3 in: Brandt, Felix; Conitzer, Vincent; Endriss, Ulle; Lang, Jérôme; Procaccia, Ariel D. (2016) (in en). Handbook of Computational Social Choice. Cambridge University Press. ISBN 9781107060432. https://books.google.com/books?id=nMHgCwAAQBAJ. (free online version)
- ↑ McGarvey, David C. (1953). "A Theorem on the Construction of Voting Paradoxes". Econometrica 21 (4): 608–610. doi:10.2307/1907926.
- ↑ Stearns, Richard (1959). "The Voting Problem". The American Mathematical Monthly 66 (9): 761–763. doi:10.2307/2310461.
- ↑ Austen-Smith, D. and J. Banks, Positive Political theory, 1999, The University of Michigan Press.
References
- Bang-Jensen, J. (1997), "Hamiltonian Cycles Avoiding Prescribed Arcs in Tournaments", Combinatorics, Probability and Computing 6: 255–261.
- Bar-Noy, A.; Naor, J. (1990), "Sorting, Minimal Feedback Sets and Hamilton Paths in Tournaments", SIAM Journal on Discrete Mathematics 3 (1): 7–20, doi:10.1137/0403002.
- Camion, Paul (1959), "Chemins et circuits hamiltoniens des graphes complets" (in French), Comptes Rendus de l'Académie des Sciences de Paris 249: 2151–2152, https://gallica.bnf.fr/ark:/12148/bpt6k731d/f1025.item.
- "On a problem in graph theory", The Mathematical Gazette 47: 220–223, 1963, http://www.renyi.hu/~p_erdos/1963-08.pdf.
- "On the representation of directed graphs as unions of orderings", Magyar Tud. Akad. Mat. Kutató Int. Közl. 9: 125–132, 1964, http://www.renyi.hu/~p_erdos/1964-22.pdf.
- Fraisse, P.; Thomassen, C. (1987), "A constructive solution to a tournament problem", Graphs and Combinatorics 3: 239–250.
- "A constructive solution to a tournament problem", Canadian Mathematical Bulletin 14: 45–48, 1971, doi:10.4153/cmb-1971-007-1.
- "The theory of round robin tournaments", American Mathematical Monthly 73 (3): 231–246, 1966, doi:10.2307/2315334.
- Havet, Frédéric (2013), "Section 3.1: Gallai–Roy Theorem and related results", Orientations and colouring of graphs, Lecture notes for the summer school SGT 2013 in Oléron, France, pp. 15–19, https://oc.g-scop.grenoble-inp.fr/conf/sgt2013/oleron.pdf
- Landau, H.G. (1953), "On dominance relations and the structure of animal societies. III. The condition for a score structure", Bulletin of Mathematical Biophysics 15 (2): 143–148, doi:10.1007/BF02476378.
- Laslier, J.-F. (1997), Tournament Solutions and Majority Voting, Springer.
- Moon, J. W. (1966), "On subtournaments of a tournament", Canadian Mathematical Bulletin 9 (3): 297–301, doi:10.4153/CMB-1966-038-7, http://cms.math.ca/cmb/v9/p297.
- Rédei, László (1934), "Ein kombinatorischer Satz", Acta Litteraria Szeged 7: 39–43.
- Reid, K.B.; Parker, E.T. (1970), "Disproof of a conjecture of Erdös and Moser", Journal of Combinatorial Theory 9 (3): 225–238, doi:10.1016/S0021-9800(70)80061-8.
- "On a problem of Schütte and Erdős", The Mathematical Gazette 49: 290–293, 1965, doi:10.2307/3612854.
- Takács, Lajos (1991), "A Bernoulli Excursion and Its Various Applications", Advances in Applied Probability (Applied Probability Trust) 23 (3): 557–585, doi:10.2307/1427622.
- Thomassen, Carsten (1980), "Hamiltonian-Connected Tournaments", Journal of Combinatorial Theory, Series B 28 (2): 142–163, doi:10.1016/0095-8956(80)90061-1.
- Yao, T.X. (1989), "On Reid conjecture of score sets for tournaments", Chinese Sci. Bull. 34: 804–808.
 |



