Physics:Physical geodesy
| Geodesy |
|---|
 |
Physical geodesy is the study of the physical properties of Earth's gravity and its potential field (the geopotential), with a view to their application in geodesy.
Measurement procedure
Traditional geodetic instruments such as theodolites rely on the gravity field for orienting their vertical axis along the local plumb line or local vertical direction with the aid of a spirit level. After that, vertical angles (zenith angles or, alternatively, elevation angles) are obtained with respect to this local vertical, and horizontal angles in the plane of the local horizon, perpendicular to the vertical.
Levelling instruments again are used to obtain geopotential differences between points on the Earth's surface. These can then be expressed as "height" differences by conversion to metric units.
Units
Gravity is commonly measured in units of m·s−2 (metres per second squared). This also can be expressed (multiplying by the gravitational constant G in order to change units) as newtons per kilogram of attracted mass.
Potential is expressed as gravity times distance, m2·s−2. Travelling one metre in the direction of a gravity vector of strength 1 m·s−2 will increase your potential by 1 m2·s−2. Again employing G as a multiplier, the units can be changed to joules per kilogram of attracted mass.
A more convenient unit is the GPU, or geopotential unit: it equals 10 m2·s−2. This means that travelling one metre in the vertical direction, i.e., the direction of the 9.8 m·s−2 ambient gravity, will approximately change your potential by 1 GPU. Which again means that the difference in geopotential, in GPU, of a point with that of sea level can be used as a rough measure of height "above sea level" in metres.
Gravity
Potential fields
Geoid
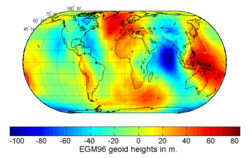
Due to the irregularity of the Earth's true gravity field, the equilibrium figure of sea water, or the geoid, will also be of irregular form. In some places, like west of Ireland, the geoid—mathematical mean sea level—sticks out as much as 100 m above the regular, rotationally symmetric reference ellipsoid of GRS80; in other places, like close to Sri Lanka, it dives under the ellipsoid by nearly the same amount. The separation between the geoid and the reference ellipsoid is called the undulation of the geoid, symbol [math]\displaystyle{ N }[/math].
The geoid, or mathematical mean sea surface, is defined not only on the seas, but also under land; it is the equilibrium water surface that would result, would sea water be allowed to move freely (e.g., through tunnels) under the land. Technically, an equipotential surface of the true geopotential, chosen to coincide (on average) with mean sea level.
As mean sea level is physically realized by tide gauge bench marks on the coasts of different countries and continents, a number of slightly incompatible "near-geoids" will result, with differences of several decimetres to over one metre between them, due to the dynamic sea surface topography. These are referred to as vertical datums or height datums.
For every point on Earth, the local direction of gravity or vertical direction, materialized with the plumb line, is perpendicular to the geoid (see astrogeodetic leveling).
Geoid determination
The undulation of the geoid is closely related to the disturbing potential according to the famous Bruns' formula:
- [math]\displaystyle{ N=T/\gamma\,, }[/math]
where [math]\displaystyle{ \gamma }[/math] is the force of gravity computed from the normal field potential [math]\displaystyle{ U }[/math].
In 1849, the mathematician George Gabriel Stokes published the following formula, named after him:
- [math]\displaystyle{ N=\frac{R}{4\pi \gamma_0}\iint_\sigma \Delta g \,S(\psi)\, d\sigma. }[/math]
In Stokes' formula or Stokes' integral, [math]\displaystyle{ \Delta g }[/math] stands for gravity anomaly, differences between true and normal (reference) gravity, and S is the Stokes function, a kernel function derived by Stokes in closed analytical form.[1]
Note that determining [math]\displaystyle{ N }[/math] anywhere on Earth by this formula requires [math]\displaystyle{ \Delta g }[/math] to be known everywhere on Earth, including oceans, polar areas, and deserts. For terrestrial gravimetric measurements this is a near-impossibility, in spite of close international co-operation within the International Association of Geodesy (IAG), e.g., through the International Gravity Bureau (BGI, Bureau Gravimétrique International).
Another approach is to combine multiple information sources: not just terrestrial gravimetry, but also satellite geodetic data on the figure of the Earth, from analysis of satellite orbital perturbations, and lately from satellite gravity missions such as GOCE and GRACE. In such combination solutions, the low-resolution part of the geoid solution is provided by the satellite data, while a 'tuned' version of the above Stokes equation is used to calculate the high-resolution part, from terrestrial gravimetric data from a neighbourhood of the evaluation point only.
Gravity anomalies
Above we already made use of gravity anomalies [math]\displaystyle{ \Delta g }[/math]. These are computed as the differences between true (observed) gravity [math]\displaystyle{ g=\|\vec{g}\| }[/math], and calculated (normal) gravity [math]\displaystyle{ \gamma=\|\vec{\gamma}\|=\|\nabla U\| }[/math]. (This is an oversimplification; in practice the location in space at which γ is evaluated will differ slightly from that where g has been measured.) We thus get
- [math]\displaystyle{ \Delta g = g - \gamma.\, }[/math]
These anomalies are called free-air anomalies, and are the ones to be used in the above Stokes equation.
In geophysics, these anomalies are often further reduced by removing from them the attraction of the topography, which for a flat, horizontal plate (Bouguer plate) of thickness H is given by
- [math]\displaystyle{ a_B=2\pi G\rho H,\, }[/math]
The Bouguer reduction to be applied as follows:
- [math]\displaystyle{ \Delta g_B = \Delta g_{FA} - a_B,\, }[/math]
so-called Bouguer anomalies. Here, [math]\displaystyle{ \Delta g_{FA} }[/math] is our earlier [math]\displaystyle{ \Delta g }[/math], the free-air anomaly.
In case the terrain is not a flat plate (the usual case!) we use for H the local terrain height value but apply a further correction called the terrain correction.
See also
- Dynamic height
- Friedrich Robert Helmert
- Geophysics
- Gravity of Earth
- Gravimetry
- LAGEOS
- Mikhail Molodenskii
- Normal height
- Orthometric height
- Satellite geodesy
References
- ↑ Wang, Yan Ming (2016). "Geodetic Boundary Value Problems". Encyclopedia of Geodesy. Cham: Springer International Publishing. pp. 1–8. doi:10.1007/978-3-319-02370-0_42-1. ISBN 978-3-319-02370-0.
Further reading
- B. Hofmann-Wellenhof and H. Moritz, Physical Geodesy, Springer-Verlag Wien, 2005. (This text is an updated edition of the 1967 classic by W.A. Heiskanen and H. Moritz).
 |


