Null vector
In mathematics, given a vector space X with an associated quadratic form q, written (X, q), a null vector or isotropic vector is a non-zero element x of X for which q(x) = 0.
In the theory of real bilinear forms, definite quadratic forms and isotropic quadratic forms are distinct. They are distinguished in that only for the latter does there exist a nonzero null vector.
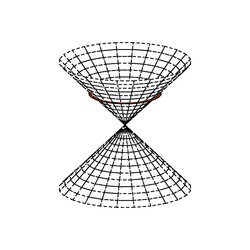
A quadratic space (X, q) which has a null vector is called a pseudo-Euclidean space.
A pseudo-Euclidean vector space may be decomposed (non-uniquely) into orthogonal subspaces A and B, X = A + B, where q is positive-definite on A and negative-definite on B. The null cone, or isotropic cone, of X consists of the union of balanced spheres: [math]\displaystyle{ \bigcup_{r \geq 0} \{x = a + b : q(a) = -q(b) = r, a \in A, b \in B \}. }[/math] The null cone is also the union of the isotropic lines through the origin.
Split algebras
A composition algebra with a null vector is a split algebra.[1]
In a composition algebra (A, +, ×, *), the quadratic form is q(x) = x x*. When x is a null vector then there is no multiplicative inverse for x, and since x ≠ 0, A is not a division algebra.
In the Cayley–Dickson construction, the split algebras arise in the series bicomplex numbers, biquaternions, and bioctonions, which uses the complex number field [math]\displaystyle{ \Complex }[/math] as the foundation of this doubling construction due to L. E. Dickson (1919). In particular, these algebras have two imaginary units, which commute so their product, when squared, yields +1:
- [math]\displaystyle{ (hi)^2 = h^2 i^2 = (-1)(-1) = +1 . }[/math] Then
- [math]\displaystyle{ (1 + hi)(1 + hi)^* = (1 +hi)(1 - hi) = 1 - (hi)^2 = 0 }[/math] so 1 + hi is a null vector.
The real subalgebras, split complex numbers, split quaternions, and split-octonions, with their null cones representing the light tracking into and out of 0 ∈ A, suggest spacetime topology.
Examples
The light-like vectors of Minkowski space are null vectors.
The four linearly independent biquaternions l = 1 + hi, n = 1 + hj, m = 1 + hk, and m∗ = 1 – hk are null vectors and { l, n, m, m∗ } can serve as a basis for the subspace used to represent spacetime. Null vectors are also used in the Newman–Penrose formalism approach to spacetime manifolds.[2]
In the Verma module of a Lie algebra there are null vectors.
References
- ↑ Arthur A. Sagle & Ralph E. Walde (1973) Introduction to Lie Groups and Lie Algebras, page 197, Academic Press
- ↑ Patrick Dolan (1968) A Singularity-free solution of the Maxwell-Einstein Equations, Communications in Mathematical Physics 9(2):161–8, especially 166, link from Project Euclid
- Dubrovin, B. A.; Fomenko, A. T.; Novikov, S. P. (1984). Modern Geometry: Methods and Applications. Springer. p. 50. ISBN 0-387-90872-2. https://archive.org/details/moderngeometryme000dubr.
- Shaw, Ronald (1982). Linear Algebra and Group Representations. 1. Academic Press. p. 151. ISBN 0-12-639201-3. https://books.google.com/books?id=C6DgAAAAMAAJ.
- Neville, E. H. (Eric Harold) (1922). Prolegomena to Analytical Geometry in Anisotropic Euclidean Space of Three Dimensions. Cambridge University Press. p. 204. https://archive.org/details/prolegomenatoana00nevi.
 |