Normal-inverse-gamma distribution

normal-inverse-gamma

Probability density function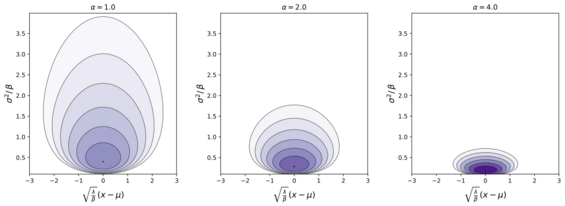
Parameters	[math]\displaystyle{ \mu\, }[/math] location (real) [math]\displaystyle{ \lambda \gt 0\, }[/math] (real) [math]\displaystyle{ \alpha \gt 0\, }[/math] (real) [math]\displaystyle{ \beta \gt 0\, }[/math] (real)
Support	[math]\displaystyle{ x \in (-\infty, \infty)\,\!, \; \sigma^2 \in (0,\infty) }[/math]
PDF	[math]\displaystyle{ \frac{ \sqrt{ \lambda } }{ \sqrt{ 2 \pi \sigma^2 }} \frac{ \beta^\alpha }{ \Gamma( \alpha ) } \left( \frac{1}{\sigma^2 } \right)^{\alpha + 1} \exp \left( -\frac { 2\beta + \lambda (x - \mu)^2} {2\sigma^2}\right) }[/math]
Mean	[math]\displaystyle{ \operatorname{E}[x] = \mu }[/math] [math]\displaystyle{ \operatorname{E}[\sigma^2] = \frac{\beta}{\alpha - 1} }[/math], for [math]\displaystyle{ \alpha \gt 1 }[/math]
Mode	[math]\displaystyle{ x = \mu \; \textrm{(univariate)}, x = \boldsymbol{\mu} \; \textrm{(multivariate)} }[/math] [math]\displaystyle{ \sigma^2 = \frac{\beta}{\alpha + 1 + 1/2} \; \textrm{(univariate)}, \sigma^2 = \frac{\beta}{\alpha + 1 + k/2} \; \textrm{(multivariate)} }[/math]
Variance	[math]\displaystyle{ \operatorname{Var}[x] = \frac{\beta}{(\alpha -1)\lambda} }[/math], for [math]\displaystyle{ \alpha \gt 1 }[/math] [math]\displaystyle{ \operatorname{Var}[\sigma^2] = \frac{\beta^2}{(\alpha -1)^2(\alpha -2)} }[/math], for [math]\displaystyle{ \alpha \gt 2 }[/math] [math]\displaystyle{ \operatorname{Cov}[x, \sigma^2] = 0 }[/math], for [math]\displaystyle{ \alpha \gt 1 }[/math]

In probability theory and statistics, the normal-inverse-gamma distribution (or Gaussian-inverse-gamma distribution) is a four-parameter family of multivariate continuous probability distributions. It is the conjugate prior of a normal distribution with unknown mean and variance.

Definition

Suppose

[math]\displaystyle{ x \mid \sigma^2, \mu, \lambda\sim \mathrm{N}(\mu,\sigma^2 / \lambda) \,\! }[/math]

has a normal distribution with mean [math]\displaystyle{ \mu }[/math] and variance [math]\displaystyle{ \sigma^2 / \lambda }[/math], where

[math]\displaystyle{ \sigma^2\mid\alpha, \beta \sim \Gamma^{-1}(\alpha,\beta) \! }[/math]

has an inverse-gamma distribution. Then [math]\displaystyle{ (x,\sigma^2) }[/math] has a normal-inverse-gamma distribution, denoted as

[math]\displaystyle{ (x,\sigma^2) \sim \text{N-}\Gamma^{-1}(\mu,\lambda,\alpha,\beta) \! . }[/math]

([math]\displaystyle{ \text{NIG} }[/math] is also used instead of [math]\displaystyle{ \text{N-}\Gamma^{-1}. }[/math])

The normal-inverse-Wishart distribution is a generalization of the normal-inverse-gamma distribution that is defined over multivariate random variables.

Characterization

Probability density function

[math]\displaystyle{ f(x,\sigma^2\mid\mu,\lambda,\alpha,\beta) = \frac {\sqrt{\lambda}} {\sigma\sqrt{2\pi} } \, \frac{\beta^\alpha}{\Gamma(\alpha)} \, \left( \frac{1}{\sigma^2} \right)^{\alpha + 1} \exp \left( -\frac { 2\beta + \lambda(x - \mu)^2} {2\sigma^2} \right) }[/math]

For the multivariate form where [math]\displaystyle{ \mathbf{x} }[/math] is a [math]\displaystyle{ k \times 1 }[/math] random vector,

[math]\displaystyle{ f(\mathbf{x},\sigma^2\mid\mu,\mathbf{V}^{-1},\alpha,\beta) = |\mathbf{V}|^{-1/2} {(2\pi)^{-k/2} } \, \frac{\beta^\alpha}{\Gamma(\alpha)} \, \left( \frac{1}{\sigma^2} \right)^{\alpha + 1 + k/2} \exp \left( -\frac { 2\beta + (\mathbf{x} - \boldsymbol{\mu})^T \mathbf{V}^{-1} (\mathbf{x} - \boldsymbol{\mu})} {2\sigma^2} \right). }[/math]

where [math]\displaystyle{ |\mathbf{V}| }[/math] is the determinant of the [math]\displaystyle{ k \times k }[/math] matrix [math]\displaystyle{ \mathbf{V} }[/math]. Note how this last equation reduces to the first form if [math]\displaystyle{ k = 1 }[/math] so that [math]\displaystyle{ \mathbf{x}, \mathbf{V}, \boldsymbol{\mu} }[/math] are scalars.

Alternative parameterization

It is also possible to let [math]\displaystyle{ \gamma = 1 / \lambda }[/math] in which case the pdf becomes

[math]\displaystyle{ f(x,\sigma^2\mid\mu,\gamma,\alpha,\beta) = \frac {1} {\sigma\sqrt{2\pi\gamma} } \, \frac{\beta^\alpha}{\Gamma(\alpha)} \, \left( \frac{1}{\sigma^2} \right)^{\alpha + 1} \exp \left( -\frac{2\gamma\beta + (x - \mu)^2}{2\gamma \sigma^2} \right) }[/math]

In the multivariate form, the corresponding change would be to regard the covariance matrix [math]\displaystyle{ \mathbf{V} }[/math] instead of its inverse [math]\displaystyle{ \mathbf{V}^{-1} }[/math] as a parameter.

Cumulative distribution function

[math]\displaystyle{ F(x,\sigma^2\mid\mu,\lambda,\alpha,\beta) = \frac{e^{-\frac{\beta}{\sigma^2}} \left(\frac{\beta }{\sigma ^2}\right)^\alpha \left(\operatorname{erf}\left(\frac{\sqrt{\lambda} (x-\mu )}{\sqrt{2} \sigma }\right)+1\right)}{2 \sigma^2 \Gamma (\alpha)} }[/math]

Properties

Marginal distributions

Given [math]\displaystyle{ (x,\sigma^2) \sim \text{N-}\Gamma^{-1}(\mu,\lambda,\alpha,\beta) \! . }[/math] as above, [math]\displaystyle{ \sigma^2 }[/math] by itself follows an inverse gamma distribution:

[math]\displaystyle{ \sigma^2 \sim \Gamma^{-1}(\alpha,\beta) \! }[/math]

while [math]\displaystyle{ \sqrt{\frac{\alpha\lambda}{\beta}} (x - \mu) }[/math] follows a t distribution with [math]\displaystyle{ 2 \alpha }[/math] degrees of freedom.

Proof for [math]\displaystyle{ \lambda = 1 }[/math]

For [math]\displaystyle{ \lambda = 1 }[/math] probability density function is

[math]\displaystyle{ f(x,\sigma^2 \mid \mu,\alpha,\beta) = \frac {1} {\sigma\sqrt{2\pi} } \, \frac{\beta^\alpha}{\Gamma(\alpha)} \, \left( \frac{1}{\sigma^2} \right)^{\alpha + 1} \exp \left( -\frac { 2\beta + (x - \mu)^2} {2\sigma^2} \right) }[/math]

Marginal distribution over [math]\displaystyle{ x }[/math] is

[math]\displaystyle{ \begin{align} f(x \mid \mu,\alpha,\beta) & = \int_0^\infty d\sigma^2 f(x,\sigma^2\mid\mu,\alpha,\beta) \\ & = \frac {1} {\sqrt{2\pi} } \, \frac{\beta^\alpha}{\Gamma(\alpha)} \int_0^\infty d\sigma^2 \left( \frac{1}{\sigma^2} \right)^{\alpha + 1/2 + 1} \exp \left( -\frac { 2\beta + (x - \mu)^2} {2\sigma^2} \right) \end{align} }[/math]

Except for normalization factor, expression under the integral coincides with Inverse-gamma distribution

[math]\displaystyle{ \Gamma^{-1}(x; a, b) = \frac{b^a}{\Gamma(a)}\frac{e^{-b/x}}{{x}^{a+1}} , }[/math]

with [math]\displaystyle{ x=\sigma^2 }[/math], [math]\displaystyle{ a = \alpha + 1/2 }[/math], [math]\displaystyle{ b = \frac { 2\beta + (x - \mu)^2} {2} }[/math].

Since [math]\displaystyle{ \int_0^\infty dx \Gamma^{-1}(x; a, b) = 1, \quad \int_0^\infty dx x^{-(a+1)} e^{-b/x} = \Gamma(a) b^{-a} }[/math], and

[math]\displaystyle{ \int_0^\infty d\sigma^2 \left( \frac{1}{\sigma^2} \right)^{\alpha + 1/2 + 1} \exp \left( -\frac { 2\beta + (x - \mu)^2} {2\sigma^2} \right) = \Gamma(\alpha + 1/2) \left(\frac { 2\beta + (x - \mu)^2} {2} \right)^{-(\alpha + 1/2)} }[/math]

Substituting this expression and factoring dependence on [math]\displaystyle{ x }[/math],

[math]\displaystyle{ f(x \mid \mu,\alpha,\beta) \propto_{x} \left(1 + \frac{(x - \mu)^2}{2 \beta} \right)^{-(\alpha + 1/2)} . }[/math]

Shape of generalized Student's t-distribution is

[math]\displaystyle{ t(x | \nu,\hat{\mu},\hat{\sigma}^2) \propto_x \left(1+\frac{1}{\nu} \frac{ (x-\hat{\mu})^2 }{\hat{\sigma}^2 } \right)^{-(\nu+1)/2} }[/math].

Marginal distribution [math]\displaystyle{ f(x \mid \mu,\alpha,\beta) }[/math] follows t-distribution with [math]\displaystyle{ 2 \alpha }[/math] degrees of freedom

[math]\displaystyle{ f(x \mid \mu,\alpha,\beta) = t(x | \nu=2 \alpha, \hat{\mu}=\mu, \hat{\sigma}^2=\beta/\alpha ) }[/math].

In the multivariate case, the marginal distribution of [math]\displaystyle{ \mathbf{x} }[/math] is a multivariate t distribution:

[math]\displaystyle{ \mathbf{x} \sim t_{2\alpha}(\boldsymbol{\mu}, \frac{\beta}{\alpha} \mathbf{V}) \! }[/math]

Scaling

Suppose

[math]\displaystyle{ (x,\sigma^2) \sim \text{N-}\Gamma^{-1}(\mu,\lambda,\alpha,\beta) \! . }[/math]

Then for [math]\displaystyle{ c\gt 0 }[/math],

[math]\displaystyle{ (cx,c\sigma^2) \sim \text{N-}\Gamma^{-1}(c\mu,\lambda/c,\alpha,c\beta) \! . }[/math]

Proof: To prove this let [math]\displaystyle{ (x,\sigma^2) \sim \text{N-}\Gamma^{-1}(\mu,\lambda,\alpha,\beta) }[/math] and fix [math]\displaystyle{ c\gt 0 }[/math]. Defining [math]\displaystyle{ Y=(Y_1,Y_2)=(cx,c \sigma^2) }[/math], observe that the PDF of the random variable [math]\displaystyle{ Y }[/math] evaluated at [math]\displaystyle{ (y_1,y_2) }[/math] is given by [math]\displaystyle{ 1/c^2 }[/math] times the PDF of a [math]\displaystyle{ \text{N-}\Gamma^{-1}(\mu,\lambda,\alpha,\beta) }[/math] random variable evaluated at [math]\displaystyle{ (y_1/c,y_2/c) }[/math]. Hence the PDF of [math]\displaystyle{ Y }[/math] evaluated at [math]\displaystyle{ (y_1,y_2) }[/math] is given by :[math]\displaystyle{ f_Y(y_1,y_2)=\frac{1}{c^2} \frac {\sqrt{\lambda}} {\sqrt{2\pi y_2/c} } \, \frac{\beta^\alpha}{\Gamma(\alpha)} \, \left( \frac{1}{y_2/c} \right)^{\alpha + 1} \exp \left( -\frac { 2\beta + \lambda(y_1/c - \mu)^2} {2y_2/c} \right) = \frac {\sqrt{\lambda/c}} {\sqrt{2\pi y_2} } \, \frac{(c\beta)^\alpha}{\Gamma(\alpha)} \, \left( \frac{1}{y_2} \right)^{\alpha + 1} \exp \left( -\frac { 2c\beta + (\lambda/c) \, (y_1 - c\mu)^2} {2y_2} \right).\! }[/math]

The right hand expression is the PDF for a [math]\displaystyle{ \text{N-}\Gamma^{-1}(c\mu,\lambda/c,\alpha,c\beta) }[/math] random variable evaluated at [math]\displaystyle{ (y_1,y_2) }[/math], which completes the proof.

Exponential family

Normal-inverse-gamma distributions form an exponential family with natural parameters [math]\displaystyle{ \textstyle\theta_1=\frac{-\lambda}{2} }[/math], [math]\displaystyle{ \textstyle\theta_2=\lambda \mu }[/math], [math]\displaystyle{ \textstyle\theta_3=\alpha }[/math], and [math]\displaystyle{ \textstyle\theta_4=-\beta+\frac{-\lambda \mu^2}{2} }[/math] and sufficient statistics [math]\displaystyle{ \textstyle T_1=\frac{x^2}{\sigma^2} }[/math], [math]\displaystyle{ \textstyle T_2=\frac{x}{\sigma^2} }[/math], [math]\displaystyle{ \textstyle T_3=\log \big( \frac{1}{\sigma^2} \big) }[/math], and [math]\displaystyle{ \textstyle T_4=\frac{1}{\sigma^2} }[/math].

Kullback–Leibler divergence

Measures difference between two distributions.

Posterior distribution of the parameters

See the articles on normal-gamma distribution and conjugate prior.

Interpretation of the parameters

See the articles on normal-gamma distribution and conjugate prior.

Generating normal-inverse-gamma random variates

Generation of random variates is straightforward:

1. Sample [math]\displaystyle{ \sigma^2 }[/math] from an inverse gamma distribution with parameters [math]\displaystyle{ \alpha }[/math] and [math]\displaystyle{ \beta }[/math]
2. Sample [math]\displaystyle{ x }[/math] from a normal distribution with mean [math]\displaystyle{ \mu }[/math] and variance [math]\displaystyle{ \sigma^2/\lambda }[/math]

Related distributions

• The normal-gamma distribution is the same distribution parameterized by precision rather than variance
• A generalization of this distribution which allows for a multivariate mean and a completely unknown positive-definite covariance matrix [math]\displaystyle{ \sigma^2 \mathbf{V} }[/math] (whereas in the multivariate inverse-gamma distribution the covariance matrix is regarded as known up to the scale factor [math]\displaystyle{ \sigma^2 }[/math]) is the normal-inverse-Wishart distribution

See also

• Compound probability distribution

References

• Denison, David G. T.; Holmes, Christopher C.; Mallick, Bani K.; Smith, Adrian F. M. (2002) Bayesian Methods for Nonlinear Classification and Regression, Wiley. ISBN:0471490369
• Koch, Karl-Rudolf (2007) Introduction to Bayesian Statistics (2nd Edition), Springer. ISBN:354072723X