Meyer wavelet
The Meyer wavelet is an orthogonal wavelet proposed by Yves Meyer.[1] As a type of a continuous wavelet, it has been applied in a number of cases, such as in adaptive filters,[2] fractal random fields,[3] and multi-fault classification.[4]
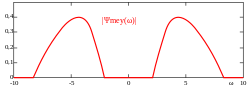
The Meyer wavelet is infinitely differentiable with infinite support and defined in frequency domain in terms of function [math]\displaystyle{ \nu }[/math] as
- [math]\displaystyle{ \Psi(\omega) := \begin{cases} \frac {1}{\sqrt{2\pi}} \sin\left(\frac {\pi}{2} \nu \left(\frac{3|\omega|}{2\pi} -1\right)\right) e^{j\omega/2} & \text{if } 2 \pi /3\lt |\omega|\lt 4 \pi /3, \\ \frac {1}{\sqrt{2\pi}} \cos\left(\frac {\pi}{2} \nu \left(\frac{3| \omega|}{4 \pi}-1\right)\right) e^{j \omega/2} & \text{if } 4 \pi /3\lt | \omega|\lt 8 \pi /3, \\ 0 & \text{otherwise}, \end{cases} }[/math]
where
- [math]\displaystyle{ \nu (x) := \begin{cases} 0 & \text{if } x \lt 0, \\ x & \text{if } 0\lt x \lt 1, \\ 1 & \text{if } x \gt 1. \end{cases} }[/math]
There are many different ways for defining this auxiliary function, which yields variants of the Meyer wavelet. For instance, another standard implementation adopts
- [math]\displaystyle{ \nu (x) := \begin{cases} x^4 (35 - 84x + 70x^2 - 20x^3) & \text{if } 0 \lt x \lt 1, \\ 0 & \text{otherwise}. \end{cases} }[/math]
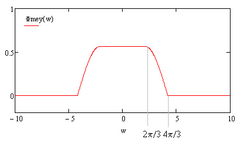
The Meyer scale function is given by
- [math]\displaystyle{ \Phi(\omega) := \begin{cases} \frac{1}{\sqrt{2\pi}} & \text{if } | \omega| \lt 2 \pi/3, \\ \frac{1}{\sqrt{2\pi}} \cos\left(\frac{\pi}{2} \nu \left(\frac{3|\omega|}{2\pi} - 1\right) \right) & \text{if } 2\pi/3 \lt |\omega| \lt 4\pi/3, \\ 0 & \text{otherwise}. \end{cases} }[/math]
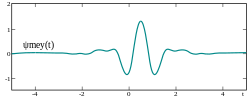
In the time domain, the waveform of the Meyer mother-wavelet has the shape as shown in the following figure:
Close expressions
Valenzuela and de Oliveira [5] give the explicit expressions of Meyer wavelet and scale functions:
- [math]\displaystyle{ \phi(t) = \begin{cases} \frac{2}{3} + \frac{4}{3\pi} & t = 0, \\ \frac{\sin(\frac{2\pi}{3}t) + \frac{4}{3}t\cos(\frac{4\pi}{3}t)}{\pi t - \frac{16\pi}{9}t^3} & \text{otherwise}, \end{cases} }[/math]
and
- [math]\displaystyle{ \psi(t) = \psi_1(t) + \psi_2(t), }[/math]
where
- [math]\displaystyle{ \psi_1(t) = \frac{\frac{4}{3\pi}(t - \frac12)\cos[\frac{2\pi}{3}(t - \frac12)] - \frac{1}{\pi}\sin[\frac{4\pi}{3}(t - \frac12)]}{(t - \frac12) - \frac{16}{9}(t - \frac12)^3}, }[/math]
- [math]\displaystyle{ \psi_2(t) = \frac{\frac{8}{3\pi}(t - \frac12)\cos[\frac{8\pi}{3}(t - \frac12)] + \frac{1}{\pi}\sin[\frac{4\pi}{3}(t - \frac12)]}{(t - \frac12) - \frac{64}{9}(t - \frac12)^3}. }[/math]
References
- ↑ Meyer, Yves (1990). Ondelettes et opérateurs: Ondelettes. Hermann. ISBN 9782705661250.
- ↑ Xu, L.; Zhang, D.; Wang, K. (2005). "Wavelet-based cascaded adaptive filter for removing baseline drift in pulse waveforms". IEEE Transactions on Biomedical Engineering 52 (11): 1973–1975. doi:10.1109/tbme.2005.856296. PMID 16285403.
- ↑ Elliott, Jr., F. W.; Horntrop, D. J.; Majda, A. J. (1997). "A Fourier-Wavelet Monte Carlo method for fractal random fields". Journal of Computational Physics 132 (2): 384–408. doi:10.1006/jcph.1996.5647. Bibcode: 1997JCoPh.132..384E.
- ↑ Abbasion, S. (2007). "Rolling element bearings multi-fault classification based on the wavelet denoising and support vector machine". Mechanical Systems and Signal Processing 21 (7): 2933–2945. doi:10.1016/j.ymssp.2007.02.003. Bibcode: 2007MSSP...21.2933A.
- ↑ Valenzuela, Victor Vermehren; de Oliveira, H. M. (2015). "Close expressions for Meyer Wavelet and Scale Function". Anais de XXXIII Simpósio Brasileiro de Telecomunicações. p. 4. doi:10.14209/SBRT.2015.2.
- Daubechies, Ingrid (September 1992). Ten Lectures on Wavelets (CBMS-NSF conference series in applied mathematics) (SIAM ed.). Springer-Verlag. pp. 117–119, 137–138, 152–155. ISBN 978-0-89871-274-2. https://archive.org/details/tenlecturesonwav0000daub/page/117.
External links
| Wikimedia Commons has media related to Wavelet. |
 |