Matching distance
In mathematics, the matching distance[1][2] is a metric on the space of size functions.
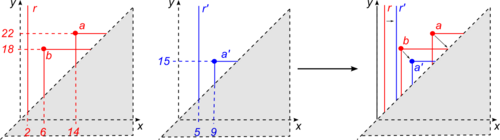
The core of the definition of matching distance is the observation that the information contained in a size function can be combinatorially stored in a formal series of lines and points of the plane, called respectively cornerlines and cornerpoints.
Given two size functions [math]\displaystyle{ \ell_1 }[/math] and [math]\displaystyle{ \ell_2 }[/math], let [math]\displaystyle{ C_1 }[/math] (resp. [math]\displaystyle{ C_2 }[/math]) be the multiset of all cornerpoints and cornerlines for [math]\displaystyle{ \ell_1 }[/math] (resp. [math]\displaystyle{ \ell_2 }[/math]) counted with their multiplicities, augmented by adding a countable infinity of points of the diagonal [math]\displaystyle{ \{(x,y)\in \R^2: x=y\} }[/math].
The matching distance between [math]\displaystyle{ \ell_1 }[/math] and [math]\displaystyle{ \ell_2 }[/math] is given by [math]\displaystyle{ d_\text{match}(\ell_1, \ell_2)=\min_\sigma\max_{p\in C_1}\delta (p,\sigma(p)) }[/math] where [math]\displaystyle{ \sigma }[/math] varies among all the bijections between [math]\displaystyle{ C_1 }[/math] and [math]\displaystyle{ C_2 }[/math] and
- [math]\displaystyle{ \delta\left((x,y),(x',y')\right)=\min\left\{\max \{|x-x'|,|y-y'|\}, \max\left\{\frac{y-x}{2},\frac{y'-x'}{2}\right\}\right\}. }[/math]
Roughly speaking, the matching distance [math]\displaystyle{ d_\text{match} }[/math] between two size functions is the minimum, over all the matchings between the cornerpoints of the two size functions, of the maximum of the [math]\displaystyle{ L_\infty }[/math]-distances between two matched cornerpoints. Since two size functions can have a different number of cornerpoints, these can be also matched to points of the diagonal [math]\displaystyle{ \Delta }[/math]. Moreover, the definition of [math]\displaystyle{ \delta }[/math] implies that matching two points of the diagonal has no cost.
See also
References
- ↑ Michele d'Amico, Patrizio Frosini, Claudia Landi, Using matching distance in Size Theory: a survey, International Journal of Imaging Systems and Technology, 16(5):154–161, 2006.
- ↑ Michele d'Amico, Patrizio Frosini, Claudia Landi, Natural pseudo-distance and optimal matching between reduced size functions, Acta Applicandae Mathematicae, 109(2):527-554, 2010.
 |