Kaniadakis Gaussian distribution
|
Probability density function 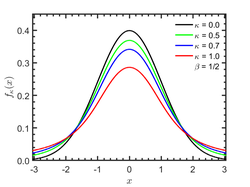 | |||
|
Cumulative distribution function 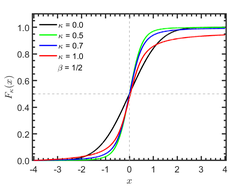 | |||
| Parameters |
[math]\displaystyle{ 0 \lt \kappa \lt 1 }[/math] shape (real) [math]\displaystyle{ \beta\gt 0 }[/math] rate (real) | ||
|---|---|---|---|
| Support | [math]\displaystyle{ x \in \mathbb{R} }[/math] | ||
| [math]\displaystyle{ Z_\kappa \exp_\kappa(-\beta x^2) \, \, \, ; \, \, \, Z_\kappa = \sqrt{\frac{2 \beta \kappa}{ \pi } } \Bigg( 1 + \frac{1}{2}\kappa \Bigg) \frac{ \Gamma \Big( \frac{1}{2 \kappa} + \frac{1}{4}\Big)}{ \Gamma \Big( \frac{1}{2 \kappa} - \frac{1}{4}\Big) } }[/math] | |||
| CDF | [math]\displaystyle{ \frac{1}{2} + \frac{1}{2} \textrm{erf}_\kappa \big( \sqrt{\beta} x\big)\ }[/math] | ||
| Mean | [math]\displaystyle{ 0 }[/math] | ||
| Median | [math]\displaystyle{ 0 }[/math] | ||
| Mode | [math]\displaystyle{ 0 }[/math] | ||
| Variance | [math]\displaystyle{ \sigma_\kappa^2 = \frac{1}{\beta} \frac{2 + \kappa}{2 - \kappa} \frac{4\kappa}{4 - 9 \kappa^2 } \left[ \frac{\Gamma \Big( \frac{1}{2\kappa} + \frac{1}{ 4 }\Big)}{\Gamma \Big( \frac{1}{2\kappa} - \frac{1}{ 4 }\Big)} \right]^2 }[/math] | ||
| Skewness | [math]\displaystyle{ 0 }[/math] | ||
| Kurtosis | [math]\displaystyle{ 3\left[\frac{\sqrt{\pi} Z_\kappa}{ 2 \beta^{2/3} \sigma_\kappa^4 } \frac{ (2 \kappa)^{-5/2} }{1+\frac{5}{2} \kappa } \frac{\Gamma \left( \frac{1}{ 2 \kappa } - \frac{5}{4} \right)}{\Gamma \left( \frac{1}{ 2 \kappa } + \frac{5}{4} \right)} -1 \right] }[/math] | ||
The Kaniadakis Gaussian distribution (also known as κ-Gaussian distribution) is a probability distribution which arises as a generalization of the Gaussian distribution from the maximization of the Kaniadakis entropy under appropriated constraints. It is one example of a Kaniadakis κ-distribution. The κ-Gaussian distribution has been applied successfully for describing several complex systems in economy,[1] geophysics,[2] astrophysics, among many others.
The κ-Gaussian distribution is a particular case of the κ-Generalized Gamma distribution.[3]
Definitions
Probability density function
The general form of the centered Kaniadakis κ-Gaussian probability density function is:[3]
- [math]\displaystyle{ f_{_{\kappa}}(x) = Z_\kappa \exp_\kappa(-\beta x^2) }[/math]
where [math]\displaystyle{ |\kappa| \lt 1 }[/math] is the entropic index associated with the Kaniadakis entropy, [math]\displaystyle{ \beta \gt 0 }[/math] is the scale parameter, and
- [math]\displaystyle{ Z_\kappa = \sqrt{\frac{2 \beta \kappa}{ \pi } } \Bigg( 1 + \frac{1}{2}\kappa \Bigg) \frac{ \Gamma \Big( \frac{1}{2 \kappa} + \frac{1}{4}\Big)}{ \Gamma \Big( \frac{1}{2 \kappa} - \frac{1}{4}\Big) } }[/math]
is the normalization constant.
The standard Normal distribution is recovered in the limit [math]\displaystyle{ \kappa \rightarrow 0. }[/math]
Cumulative distribution function
The cumulative distribution function of κ-Gaussian distribution is given by
[math]\displaystyle{ F_\kappa(x) = \frac{1}{2} + \frac{1}{2} \textrm{erf}_\kappa \big( \sqrt{\beta} x\big) }[/math]
where
[math]\displaystyle{ \textrm{erf}_\kappa(x) = \Big( 2+ \kappa \Big) \sqrt{ \frac{2 \kappa}{\pi} } \frac{\Gamma\Big( \frac{1}{2\kappa} + \frac{1}{4} \Big)}{ \Gamma\Big( \frac{1}{2\kappa} - \frac{1}{4} \Big) } \int_0^x \exp_\kappa(-t^2 ) dt }[/math]
is the Kaniadakis κ-Error function, which is a generalization of the ordinary Error function [math]\displaystyle{ \textrm{erf}(x) }[/math] as [math]\displaystyle{ \kappa \rightarrow 0 }[/math].
Properties
Moments, mean and variance
The centered κ-Gaussian distribution has a moment of odd order equal to zero, including the mean.
The variance is finite for [math]\displaystyle{ \kappa \lt 2/3 }[/math] and is given by:
- [math]\displaystyle{ \operatorname{Var}[X] = \sigma_\kappa^2 = \frac{1}{\beta} \frac{2 + \kappa}{2 - \kappa} \frac{4\kappa}{4 - 9 \kappa^2 } \left[\frac{\Gamma \left( \frac{1}{2\kappa} + \frac{1}{ 4 }\right)}{\Gamma \left( \frac{1}{2\kappa} - \frac{1}{ 4 }\right)}\right]^2 }[/math]
Kurtosis
The kurtosis of the centered κ-Gaussian distribution may be computed thought:
- [math]\displaystyle{ \operatorname{Kurt}[X] = \operatorname{E}\left[\frac{X^4}{\sigma_\kappa^4}\right] }[/math]
which can be written as
[math]\displaystyle{ \operatorname{Kurt}[X] = \frac{2 Z_\kappa}{\sigma_\kappa^4} \int_0^\infty x^4 \, \exp_\kappa \left( -\beta x^2 \right) dx }[/math]
Thus, the kurtosis of the centered κ-Gaussian distribution is given by:
[math]\displaystyle{ \operatorname{Kurt}[X] = \frac{3\sqrt \pi Z_\kappa}{ 2 \beta^{2/3} \sigma_\kappa^4 } \frac{|2 \kappa|^{-5/2}}{1+\frac{5}{2} |\kappa| } \frac{\Gamma \left( \frac{1}{|2 \kappa| } - \frac{5}{4} \right)}{\Gamma \left( \frac{1}{|2 \kappa| } + \frac{5}{4} \right)} }[/math]
or
[math]\displaystyle{ \operatorname{Kurt}[X] = \frac{ 3\beta^{11/6}\sqrt{2 \kappa} }{ 2 } \frac{|2 \kappa|^{-5/2}}{1+\frac{5}{2} |\kappa| } \Bigg( 1 + \frac{1}{2}\kappa \Bigg) \left(\frac{2 - \kappa}{2 + \kappa} \right)^2 \left( \frac{4 - 9 \kappa^2 }{4\kappa} \right)^2 \left[\frac{\Gamma \Big( \frac{1}{2\kappa} - \frac{1}{ 4 }\Big)}{\Gamma \Big( \frac{1}{2\kappa} + \frac{1}{ 4 }\Big)}\right]^3 \frac{\Gamma \left( \frac{1}{|2 \kappa| } - \frac{5}{4} \right)}{\Gamma \left( \frac{1}{|2 \kappa| } + \frac{5}{4} \right)} }[/math]
κ-Error function
Template:Infobox mathematical function
The Kaniadakis κ-Error function (or κ-Error function) is a one-parameter generalization of the ordinary error function defined as:[3]
- [math]\displaystyle{ \operatorname{erf}_\kappa(x) = \Big( 2+ \kappa \Big) \sqrt{ \frac{2 \kappa}{\pi} } \frac{\Gamma\Big( \frac{1}{2\kappa} + \frac{1}{4} \Big)}{ \Gamma\Big( \frac{1}{2\kappa} - \frac{1}{4} \Big) } \int_0^x \exp_\kappa(-t^2 ) dt }[/math]
Although the error function cannot be expressed in terms of elementary functions, numerical approximations are commonly employed.
For a random variable X distributed according to a κ-Gaussian distribution with mean 0 and standard deviation [math]\displaystyle{ \sqrt \beta }[/math], κ-Error function means the probability that X falls in the interval [math]\displaystyle{ [-x, \, x] }[/math].
Applications
The κ-Gaussian distribution has been applied in several areas, such as:
- In economy, the κ-Gaussian distribution has been applied in the analysis of financial models, accurately representing the dynamics of the processes of extreme changes in stock prices.[4]
- In inverse problems, Error laws in extreme statistics are robustly represented by κ-Gaussian distributions.[2][5][6]
- In astrophysics, stellar-residual-radial-velocity data have a Gaussian-type statistical distribution, in which the K index presents a strong relationship with the stellar-cluster ages.[7][8]
- In nuclear physics, the study of Doppler broadening function in nuclear reactors is well described by a κ-Gaussian distribution for analyzing the neutron-nuclei interaction.[9][10]
- In cosmology, for interpreting the dynamical evolution of the Friedmann–Robertson–Walker Universe.
- In plasmas physics, for analyzing the electron distribution in electron-acoustic double-layers[11] and the dispersion of Langmuir waves.[12]
See also
- Giorgio Kaniadakis
- Kaniadakis statistics
- Kaniadakis distribution
- Kaniadakis κ-Exponential distribution
- Kaniadakis κ-Gamma distribution
- Kaniadakis κ-Weibull distribution
- Kaniadakis κ-Logistic distribution
- Kaniadakis κ-Erlang distribution
References
- ↑ Moretto, Enrico; Pasquali, Sara; Trivellato, Barbara (2017). "A non-Gaussian option pricing model based on Kaniadakis exponential deformation" (in en). The European Physical Journal B 90 (10): 179. doi:10.1140/epjb/e2017-80112-x. ISSN 1434-6028. Bibcode: 2017EPJB...90..179M. http://link.springer.com/10.1140/epjb/e2017-80112-x.
- ↑ 2.0 2.1 da Silva, Sérgio Luiz E. F.; Carvalho, Pedro Tiago C.; de Araújo, João M.; Corso, Gilberto (2020-05-27). "Full-waveform inversion based on Kaniadakis statistics" (in en). Physical Review E 101 (5): 053311. doi:10.1103/PhysRevE.101.053311. ISSN 2470-0045. PMID 32575242. Bibcode: 2020PhRvE.101e3311D. https://link.aps.org/doi/10.1103/PhysRevE.101.053311.
- ↑ 3.0 3.1 3.2 Kaniadakis, G. (2021-01-01). "New power-law tailed distributions emerging in κ-statistics (a)". Europhysics Letters 133 (1): 10002. doi:10.1209/0295-5075/133/10002. ISSN 0295-5075. Bibcode: 2021EL....13310002K. https://iopscience.iop.org/article/10.1209/0295-5075/133/10002.
- ↑ Moretto, Enrico; Pasquali, Sara; Trivellato, Barbara (2017). "A non-Gaussian option pricing model based on Kaniadakis exponential deformation" (in en). The European Physical Journal B 90 (10): 179. doi:10.1140/epjb/e2017-80112-x. ISSN 1434-6028. Bibcode: 2017EPJB...90..179M. http://link.springer.com/10.1140/epjb/e2017-80112-x.
- ↑ Wada, Tatsuaki; Suyari, Hiroki (2006). "κ-generalization of Gauss' law of error" (in en). Physics Letters A 348 (3–6): 89–93. doi:10.1016/j.physleta.2005.08.086. Bibcode: 2006PhLA..348...89W. https://linkinghub.elsevier.com/retrieve/pii/S0375960105013630.
- ↑ da Silva, Sérgio Luiz E.F.; Silva, R.; dos Santos Lima, Gustavo Z.; de Araújo, João M.; Corso, Gilberto (2022). "An outlier-resistant κ -generalized approach for robust physical parameter estimation" (in en). Physica A: Statistical Mechanics and Its Applications 600: 127554. doi:10.1016/j.physa.2022.127554. Bibcode: 2022PhyA..60027554D. https://linkinghub.elsevier.com/retrieve/pii/S0378437122003855.
- ↑ Carvalho, J. C.; Silva, R.; do Nascimento jr., J. D.; Soares, B. B.; De Medeiros, J. R. (2010-09-01). "Observational measurement of open stellar clusters: A test of Kaniadakis and Tsallis statistics". EPL (Europhysics Letters) 91 (6): 69002. doi:10.1209/0295-5075/91/69002. ISSN 0295-5075. Bibcode: 2010EL.....9169002C. https://iopscience.iop.org/article/10.1209/0295-5075/91/69002.
- ↑ Carvalho, J. C.; Silva, R.; do Nascimento jr., J. D.; De Medeiros, J. R. (2008). "Power law statistics and stellar rotational velocities in the Pleiades". EPL (Europhysics Letters) 84 (5): 59001. doi:10.1209/0295-5075/84/59001. ISSN 0295-5075. Bibcode: 2008EL.....8459001C. https://iopscience.iop.org/article/10.1209/0295-5075/84/59001.
- ↑ Guedes, Guilherme; Gonçalves, Alessandro C.; Palma, Daniel A.P. (2017). "The Doppler Broadening Function using the Kaniadakis distribution" (in en). Annals of Nuclear Energy 110: 453–458. doi:10.1016/j.anucene.2017.06.057. https://linkinghub.elsevier.com/retrieve/pii/S030645491730155X.
- ↑ de Abreu, Willian V.; Gonçalves, Alessandro C.; Martinez, Aquilino S. (2019). "Analytical solution for the Doppler broadening function using the Kaniadakis distribution" (in en). Annals of Nuclear Energy 126: 262–268. doi:10.1016/j.anucene.2018.11.023. https://linkinghub.elsevier.com/retrieve/pii/S0306454918306224.
- ↑ Gougam, Leila Ait; Tribeche, Mouloud (2016). "Electron-acoustic waves in a plasma with a κ -deformed Kaniadakis electron distribution" (in en). Physics of Plasmas 23 (1): 014501. doi:10.1063/1.4939477. ISSN 1070-664X. Bibcode: 2016PhPl...23a4501G. http://aip.scitation.org/doi/10.1063/1.4939477.
- ↑ Chen, H.; Zhang, S. X.; Liu, S. Q. (2017). "The longitudinal plasmas modes of κ -deformed Kaniadakis distributed plasmas" (in en). Physics of Plasmas 24 (2): 022125. doi:10.1063/1.4976992. ISSN 1070-664X. Bibcode: 2017PhPl...24b2125C. http://aip.scitation.org/doi/10.1063/1.4976992.
External links
 |

