Join (topology)
In topology, a field of mathematics, the join of two topological spaces [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math], often denoted by [math]\displaystyle{ A\ast B }[/math] or [math]\displaystyle{ A\star B }[/math], is a topological space formed by taking the disjoint union of the two spaces, and attaching line segments joining every point in [math]\displaystyle{ A }[/math] to every point in [math]\displaystyle{ B }[/math]. The join of a space [math]\displaystyle{ A }[/math] with itself is denoted by [math]\displaystyle{ A^{\star 2} := A\star A }[/math]. The join is defined in slightly different ways in different contexts
Geometric sets
If [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math] are subsets of the Euclidean space [math]\displaystyle{ \mathbb{R}^n }[/math], then:[1](p1)
[math]\displaystyle{ A\star B\ :=\ \{ t\cdot a + (1-t)\cdot b ~|~ a\in A, b\in B, t\in [0,1]\} }[/math],
that is, the set of all line-segments between a point in [math]\displaystyle{ A }[/math] and a point in [math]\displaystyle{ B }[/math].
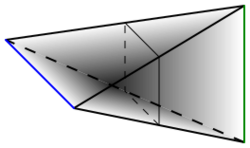
Some authors[2](p5) restrict the definition to subsets that are joinable: any two different line-segments, connecting a point of A to a point of B, meet in at most a common endpoint (that is, they do not intersect in their interior). Every two subsets can be made "joinable". For example, if [math]\displaystyle{ A }[/math] is in [math]\displaystyle{ \mathbb{R}^n }[/math] and [math]\displaystyle{ B }[/math] is in [math]\displaystyle{ \mathbb{R}^m }[/math], then [math]\displaystyle{ A\times\{ 0^m \}\times\{0\} }[/math] and [math]\displaystyle{ \{0^n \}\times B\times\{1\} }[/math] are joinable in [math]\displaystyle{ \mathbb{R}^{n+m+1} }[/math]. The figure above shows an example for m=n=1, where [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math] are line-segments.
Examples
- The join of two simplices is a simplex: the join of an n-dimensional and an m-dimensional simplex is an (m+n+1)-dimensional simplex. Some special cases are:
- The join of two disjoint points is an interval (m=n=0).
- The join of a point and an interval is a triangle (m=0, n=1).
- The join of two line segments is homeomorphic to a solid tetrahedron or disphenoid, illustrated in the figure above right (m=n=1).
- The join of a point and an (n-1)-dimensional simplex is an n-dimensional simplex.
- The join of a point and a polygon (or any polytope) is a pyramid, like the join of a point and square is a square pyramid. The join of a point and a cube is a cubic pyramid.
- The join of a point and a circle is a cone, and the join of a point and a sphere is a hypercone.
Topological spaces
If [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math] are any topological spaces, then:
- [math]\displaystyle{ A\star B\ :=\ A\sqcup_{p_0}(A\times B \times [0,1])\sqcup_{p_1}B, }[/math]
where the cylinder [math]\displaystyle{ A\times B \times [0,1] }[/math] is attached to the original spaces [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math] along the natural projections of the faces of the cylinder:
- [math]\displaystyle{ {A\times B\times \{0\}} \xrightarrow{p_0} A, }[/math]
- [math]\displaystyle{ {A\times B\times \{1\}} \xrightarrow{p_1} B. }[/math]
Usually it is implicitly assumed that [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math] are non-empty, in which case the definition is often phrased a bit differently: instead of attaching the faces of the cylinder [math]\displaystyle{ A\times B \times [0,1] }[/math] to the spaces [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math], these faces are simply collapsed in a way suggested by the attachment projections [math]\displaystyle{ p_1,p_2 }[/math]: we form the quotient space
- [math]\displaystyle{ A\star B\ :=\ (A\times B \times [0,1] )/ \sim, }[/math]
where the equivalence relation [math]\displaystyle{ \sim }[/math] is generated by
- [math]\displaystyle{ (a, b_1, 0) \sim (a, b_2, 0) \quad\mbox{for all } a \in A \mbox{ and } b_1,b_2 \in B, }[/math]
- [math]\displaystyle{ (a_1, b, 1) \sim (a_2, b, 1) \quad\mbox{for all } a_1,a_2 \in A \mbox{ and } b \in B. }[/math]
At the endpoints, this collapses [math]\displaystyle{ A\times B\times \{0\} }[/math] to [math]\displaystyle{ A }[/math] and [math]\displaystyle{ A\times B\times \{1\} }[/math] to [math]\displaystyle{ B }[/math].
If [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math] are bounded subsets of the Euclidean space [math]\displaystyle{ \mathbb{R}^n }[/math], and [math]\displaystyle{ A\subseteq U }[/math] and [math]\displaystyle{ B \subseteq V }[/math], where [math]\displaystyle{ U, V }[/math] are disjoint subspaces of [math]\displaystyle{ \mathbb{R}^n }[/math] such that the dimension of their affine hull is [math]\displaystyle{ dim U + dim V + 1 }[/math] (e.g. two non-intersecting non-parallel lines in [math]\displaystyle{ \mathbb{R}^3 }[/math]), then the topological definition reduces to the geometric definition, that is, the "geometric join" is homeomorphic to the "topological join":[3](p75)
[math]\displaystyle{ \big((A\times B \times [0,1] )/ \sim\big) \simeq \{ t\cdot a + (1-t)\cdot b ~|~ a\in A, b\in B, t\in [0,1]\} }[/math]
Abstract simplicial complexes
If [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math] are any abstract simplicial complexes, then their join is an abstract simplicial complex defined as follows:[3](p74)
- The vertex set [math]\displaystyle{ V(A\star B) }[/math] is a disjoint union of [math]\displaystyle{ V(A) }[/math] and [math]\displaystyle{ V( B) }[/math].
- The simplices of [math]\displaystyle{ A\star B }[/math] are all disjoint unions of a simplex of [math]\displaystyle{ A }[/math] with a simplex of [math]\displaystyle{ B }[/math]: [math]\displaystyle{ A\star B := \{ a\sqcup b: a\in A, b\in B \} }[/math] (in the special case in which [math]\displaystyle{ V(A) }[/math] and [math]\displaystyle{ V( B) }[/math] are disjoint, the join is simply [math]\displaystyle{ \{ a\cup b: a\in A, b\in B \} }[/math]).
Examples
- Suppose [math]\displaystyle{ A = \{ \emptyset, \{a\} \} }[/math] and [math]\displaystyle{ B = \{\emptyset, \{b\} \} }[/math], that is, two sets with a single point. Then [math]\displaystyle{ A \star B = \{ \emptyset, \{a\}, \{b\}, \{a,b\} \} }[/math], which represents a line-segment. Note that the vertex sets of A and B are disjoint; otherwise, we should have made them disjoint. For example, [math]\displaystyle{ A^{\star 2} = A \star A = \{ \emptyset, \{a_1\}, \{a_2\}, \{a_1,a_2\} \} }[/math] where a1 and a2 are two copies of the single element in V(A). Topologically, the result is the same as [math]\displaystyle{ A \star B }[/math] - a line-segment.
- Suppose [math]\displaystyle{ A = \{ \emptyset, \{a\} \} }[/math] and [math]\displaystyle{ B = \{\emptyset, \{b\}, \{c\}, \{b,c\} \} }[/math]. Then [math]\displaystyle{ A \star B = P(\{a,b,c\}) }[/math], which represents a triangle.
- Suppose [math]\displaystyle{ A = \{ \emptyset, \{a\}, \{b\} \} }[/math] and [math]\displaystyle{ B = \{\emptyset, \{c\}, \{d\} \} }[/math], that is, two sets with two discrete points. then [math]\displaystyle{ A\star B }[/math] is a complex with facets [math]\displaystyle{ \{a,c\}, \{b,c\}, \{a,d\}, \{b,d\} }[/math], which represents a "square".
The combinatorial definition is equivalent to the topological definition in the following sense:[3](p77) for every two abstract simplicial complexes [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math], [math]\displaystyle{ ||A\star B|| }[/math] is homeomorphic to [math]\displaystyle{ ||A||\star ||B|| }[/math], where [math]\displaystyle{ ||X|| }[/math] denotes any geometric realization of the complex [math]\displaystyle{ X }[/math].
Maps
Given two maps [math]\displaystyle{ f:A_1\to A_2 }[/math] and [math]\displaystyle{ g:B_1\to B_2 }[/math], their join [math]\displaystyle{ f\star g:A_1\star B_1 \to A_2\star B_2 }[/math]is defined based on the representation of each point in the join [math]\displaystyle{ A_1\star B_1 }[/math] as [math]\displaystyle{ t\cdot a +(1-t)\cdot b }[/math], for some [math]\displaystyle{ a\in A_1, b\in B_1 }[/math]:[3](p77)
[math]\displaystyle{ f\star g ~(t\cdot a +(1-t)\cdot b) ~~=~~ t\cdot f(a) + (1-t)\cdot f(b) }[/math]
Special cases
The cone of a topological space [math]\displaystyle{ X }[/math], denoted [math]\displaystyle{ CX }[/math] , is a join of [math]\displaystyle{ X }[/math] with a single point.
The suspension of a topological space [math]\displaystyle{ X }[/math], denoted [math]\displaystyle{ SX }[/math] , is a join of [math]\displaystyle{ X }[/math] with [math]\displaystyle{ S^0 }[/math] (the 0-dimensional sphere, or, the discrete space with two points).
Properties
Commutativity
The join of two spaces is commutative up to homeomorphism, i.e. [math]\displaystyle{ A\star B\cong B\star A }[/math].
Associativity
It is not true that the join operation defined above is associative up to homeomorphism for arbitrary topological spaces. However, for locally compact Hausdorff spaces [math]\displaystyle{ A, B, C }[/math] we have [math]\displaystyle{ (A\star B)\star C \cong A\star(B\star C). }[/math] Therefore, one can define the k-times join of a space with itself, [math]\displaystyle{ A^{*k} := A * \cdots * A }[/math] (k times).
It is possible to define a different join operation [math]\displaystyle{ A\; \hat{\star}\;B }[/math] which uses the same underlying set as [math]\displaystyle{ A\star B }[/math] but a different topology, and this operation is associative for all topological spaces. For locally compact Hausdorff spaces [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math], the joins [math]\displaystyle{ A\star B }[/math] and [math]\displaystyle{ A \;\hat{\star}\;B }[/math] coincide.[4]
Homotopy equivalence
If [math]\displaystyle{ A }[/math] and [math]\displaystyle{ A' }[/math] are homotopy equivalent, then [math]\displaystyle{ A\star B }[/math] and [math]\displaystyle{ A'\star B }[/math] are homotopy equivalent too.[3](p77)
Reduced join
Given basepointed CW complexes [math]\displaystyle{ (A, a_0) }[/math] and [math]\displaystyle{ (B, b_0) }[/math], the "reduced join"
- [math]\displaystyle{ \frac{A\star B}{A \star \{b_0\} \cup \{a_0\} \star B} }[/math]
is homeomorphic to the reduced suspension
[math]\displaystyle{ \Sigma(A\wedge B) }[/math]
of the smash product. Consequently, since [math]\displaystyle{ {A \star \{b_0\} \cup \{a_0\} \star B} }[/math] is contractible, there is a homotopy equivalence
- [math]\displaystyle{ A\star B\simeq \Sigma(A\wedge B). }[/math]
This equivalence establishes the isomorphism [math]\displaystyle{ \widetilde{H}_n(A\star B)\cong H_{n-1}(A\wedge B)\ \bigl( =H_{n-1}(A\times B / A\vee B)\bigr) }[/math].
Homotopical connectivity
Given two triangulable spaces [math]\displaystyle{ A, B }[/math], the homotopical connectivity ([math]\displaystyle{ \eta_{\pi} }[/math]) of their join is at least the sum of connectivities of its parts:[3](p81)
- [math]\displaystyle{ \eta_{\pi}(A*B) \geq \eta_{\pi}(A)+\eta_{\pi}(B) }[/math].
As an example, let [math]\displaystyle{ A = B = S^0 }[/math] be a set of two disconnected points. There is a 1-dimensional hole between the points, so [math]\displaystyle{ \eta_{\pi}(A)=\eta_{\pi}(B)=1 }[/math]. The join [math]\displaystyle{ A * B }[/math] is a square, which is homeomorphic to a circle that has a 2-dimensional hole, so [math]\displaystyle{ \eta_{\pi}(A * B)=2 }[/math]. The join of this square with a third copy of [math]\displaystyle{ S^0 }[/math] is a octahedron, which is homeomorphic to [math]\displaystyle{ S^2 }[/math] , whose hole is 3-dimensional. In general, the join of n copies of [math]\displaystyle{ S^0 }[/math] is homeomorphic to [math]\displaystyle{ S^{n-1} }[/math] and [math]\displaystyle{ \eta_{\pi}(S^{n-1})=n }[/math].
Deleted join
The deleted join of an abstract complex A is an abstract complex containing all disjoint unions of disjoint faces of A:[3](p112)
[math]\displaystyle{ A^{*2}_{\Delta} := \{ a_1\sqcup a_2: a_1,a_2\in A, a_1\cap a_2 = \emptyset \} }[/math]
Examples
- Suppose [math]\displaystyle{ A = \{ \emptyset, \{a\} \} }[/math] (a single point). Then [math]\displaystyle{ A^{*2}_{\Delta} := \{ \emptyset, \{a_1\}, \{a_2\} \} }[/math], that is, a discrete space with two disjoint points (recall that [math]\displaystyle{ A^{\star 2} =\{ \emptyset, \{a_1\}, \{a_2\}, \{a_1,a_2\} \} }[/math] = an interval).
- Suppose [math]\displaystyle{ A = \{ \emptyset, \{a\} ,\{b\}\} }[/math] (two points). Then [math]\displaystyle{ A^{*2}_{\Delta} }[/math] is a complex with facets [math]\displaystyle{ \{a_1, b_2\}, \{a_2, b_1\} }[/math] (two disjoint edges).
- Suppose [math]\displaystyle{ A = \{ \emptyset, \{a\} ,\{b\}, \{a,b\}\} }[/math] (an edge). Then [math]\displaystyle{ A^{*2}_{\Delta} }[/math] is a complex with facets [math]\displaystyle{ \{a_1,b_1\}, \{a_1, b_2\}, \{a_2, b_1\}, \{a_2,b_2\} }[/math] (a square). Recall that [math]\displaystyle{ A^{\star 2} }[/math] represents a solid tetrahedron.
- Suppose A represents an (n-1)-dimensional simplex (with n vertices). Then the join [math]\displaystyle{ A^{\star 2} }[/math] is a (2n-1)-dimensional simplex (with 2n vertices): it is the set of all points (x1,...,x2n) with non-negative coordinates such that x1+...+x2n=1. The deleted join [math]\displaystyle{ A^{*2}_{\Delta} }[/math] can be regarded as a subset of this simplex: it is the set of all points (x1,...,x2n) in that simplex, such that the only nonzero coordinates are some k coordinates in x1,..,xn, and the complementary n-k coordinates in xn+1,...,x2n.
Properties
The deleted join operation commutes with the join. That is, for every two abstract complexes A and B:[3]:{{{1}}}
[math]\displaystyle{ (A*B)^{*2}_{\Delta} = (A^{*2}_{\Delta}) * (B^{*2}_{\Delta}) }[/math]
Proof. Each simplex in the left-hand-side complex is of the form [math]\displaystyle{ (a_1 \sqcup b_1) \sqcup (a_2\sqcup b_2) }[/math], where [math]\displaystyle{ a_1,a_2\in A, b_1,b_2\in B }[/math], and [math]\displaystyle{ (a_1 \sqcup b_1), (a_2\sqcup b_2) }[/math] are disjoint. Due to the properties of a disjoint union, the latter condition is equivalent to: [math]\displaystyle{ a_1,a_2 }[/math] are disjoint and [math]\displaystyle{ b_1,b_2 }[/math] are disjoint.
Each simplex in the right-hand-side complex is of the form [math]\displaystyle{ (a_1 \sqcup a_2) \sqcup (b_1\sqcup b_2) }[/math], where [math]\displaystyle{ a_1,a_2\in A, b_1,b_2\in B }[/math], and [math]\displaystyle{ a_1,a_2 }[/math] are disjoint and [math]\displaystyle{ b_1,b_2 }[/math] are disjoint. So the sets of simplices on both sides are exactly the same. □
In particular, the deleted join of the n-dimensional simplex [math]\displaystyle{ \Delta^n }[/math] with itself is the n-dimensional crosspolytope, which is homeomorphic to the n-dimensional sphere [math]\displaystyle{ S^n }[/math].[3]:{{{1}}}
Generalization
The n-fold k-wise deleted join of a simplicial complex A is defined as:
[math]\displaystyle{ A^{*n}_{\Delta(k)} := \{ a_1\sqcup a_2 \sqcup\cdots \sqcup a_n: a_1,\cdots,a_n \text{ are k-wise disjoint faces of } A \} }[/math], where "k-wise disjoint" means that every subset of k have an empty intersection.
In particular, the n-fold n-wise deleted join contains all disjoint unions of n faces whose intersection is empty, and the n-fold 2-wise deleted join is smaller: it contains only the disjoint unions of n faces that are pairwise-disjoint. The 2-fold 2-wise deleted join is just the simple deleted join defined above.
The n-fold 2-wise deleted join of a discrete space with m points is called the (m,n)-chessboard complex.
See also
References
- ↑ Colin P. Rourke and Brian J. Sanderson (1982) (in en). Introduction to Piecewise-Linear Topology. New York: Springer-Verlag. doi:10.1007/978-3-642-81735-9. ISBN 978-3-540-11102-3. https://link.springer.com/book/10.1007/978-3-642-81735-9.
- ↑ Bryant, John L. (2001-01-01), Daverman, R. J.; Sher, R. B., eds., "Chapter 5 - Piecewise Linear Topology" (in en), Handbook of Geometric Topology (Amsterdam: North-Holland): pp. 219–259, ISBN 978-0-444-82432-5, https://www.sciencedirect.com/science/article/pii/B9780444824325500068, retrieved 2022-11-15
- ↑ 3.0 3.1 3.2 3.3 3.4 3.5 3.6 3.7 3.8 Template:Cite Matousek 2007, Section 4.3
- ↑ Fomenko, Anatoly; Fuchs, Dmitry (2016). Homotopical Topology (2nd ed.). Springer. pp. 20.
- Hatcher, Allen, Algebraic topology. Cambridge University Press, Cambridge, 2002. xii+544 pp. ISBN:0-521-79160-X and ISBN:0-521-79540-0
- Brown, Ronald, Topology and Groupoids Section 5.7 Joins.
 |

