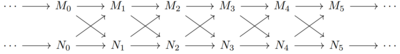Interleaving distance

Short description: Measure of distance between persistence modules

A 1-interleaving between two [math]\displaystyle{ \mathbb Z }[/math]-indexed persistence modules M and N, represented as a diagram of vector spaces and linear maps between them.

In topological data analysis, the interleaving distance is a measure of similarity between persistence modules, a common object of study in topological data analysis and persistent homology. The interleaving distance was first introduced by Frédéric Chazal et al. in 2009. since then, it and its generalizations have been a central consideration in the study of applied algebraic topology and topological data analysis.

Definition

A persistence module [math]\displaystyle{ \mathbb V }[/math] is a collection [math]\displaystyle{ (V_t \mid t \in \mathbb R) }[/math] of vector spaces indexed over the real line, along with a collection [math]\displaystyle{ (v^s_t : V_s \to V_t \mid s\leq t) }[/math] of linear maps such that [math]\displaystyle{ v^t_t }[/math] is always an isomorphism, and the relation [math]\displaystyle{ v^s_t \circ v^r_s = v^r_t }[/math] is satisfied for every [math]\displaystyle{ r\leq s \leq t }[/math]. The case of [math]\displaystyle{ \mathbb R }[/math] indexing is presented here for simplicity, though the interleaving distance can be readily adapted to more general settings, including multi-dimensional persistence modules.

Let [math]\displaystyle{ \mathbb U }[/math] and [math]\displaystyle{ \mathbb V }[/math] be persistence modules. Then for any [math]\displaystyle{ \delta \in \mathbb R }[/math], a [math]\displaystyle{ \delta }[/math]-shift is a collection [math]\displaystyle{ (\phi_t : U_t \to V_{t+\delta} \mid t \in \mathbb R) }[/math] of linear maps between the persistence modules that commute with the internal maps of [math]\displaystyle{ \mathbb U }[/math] and [math]\displaystyle{ \mathbb V }[/math].

The persistence modules [math]\displaystyle{ \mathbb U }[/math] and [math]\displaystyle{ \mathbb V }[/math] are said to be [math]\displaystyle{ \delta }[/math]-interleaved if there are [math]\displaystyle{ \delta }[/math]-shifts [math]\displaystyle{ \phi_t: U_t \to V_{t+ \delta} }[/math] and [math]\displaystyle{ \psi_t: V_t \to U_{t+ \delta} }[/math] such that the following diagrams commute for all [math]\displaystyle{ s \leq t }[/math].

It follows from the definition that if [math]\displaystyle{ \mathbb U }[/math] and [math]\displaystyle{ \mathbb V }[/math] are [math]\displaystyle{ \delta }[/math]-interleaved for some [math]\displaystyle{ \delta }[/math], then they are also [math]\displaystyle{ (\delta + \varepsilon) }[/math]-interleaved for any positive [math]\displaystyle{ \varepsilon }[/math]. Therefore, in order to find the closest interleaving between the two modules, we must take the infimum across all possible interleavings.

The interleaving distance between two persistence modules [math]\displaystyle{ \mathbb U }[/math] and [math]\displaystyle{ \mathbb V }[/math] is defined as [math]\displaystyle{ d_I (\mathbb U, \mathbb V) = \inf \{\delta \mid \mathbb U \text{ and } \mathbb V \text{ are } \delta\text{-interleaved}\} }[/math].

Properties

Metric properties

It can be shown that the interleaving distance satisfies the triangle inequality. Namely, given three persistence modules [math]\displaystyle{ \mathbb U }[/math], [math]\displaystyle{ \mathbb V }[/math], and [math]\displaystyle{ \mathbb W }[/math], the inequality [math]\displaystyle{ d_I (\mathbb U, \mathbb W) \leq d_I (\mathbb U, \mathbb V) + d_I (\mathbb V, \mathbb W) }[/math] is satisfied.

On the other hand, there are examples of persistence modules that are not isomorphic but that have interleaving distance zero. Furthermore, if no suitable [math]\displaystyle{ \delta }[/math] exists then two persistence modules are said to have infinite interleaving distance. These two properties make the interleaving distance an extended pseudometric, which means non-identical objects are allowed to have distance zero, and objects are allowed to have infinite distance, but the other properties of a proper metric are satisfied.

Further metric properties of the interleaving distance and its variants were investigated by Luis Scoccola in 2020.

Computational complexity

Computing the interleaving distance between two single-parameter persistence modules can be accomplished in polynomial time. On the other hand, it was shown in 2018 that computing the interleaving distance between two multi-dimensional persistence modules is NP-hard.