Hilbert basis (linear programming)
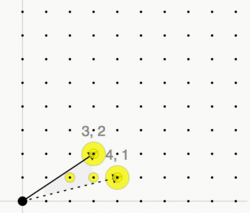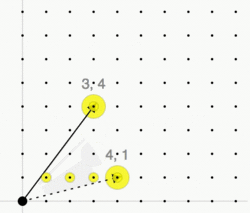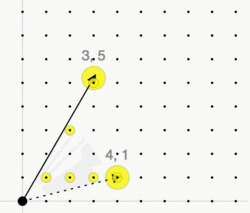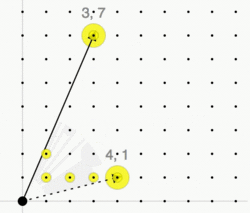
The Hilbert basis of a convex cone C is a minimal set of integer vectors such that every integer vector in C is a conical combination of the vectors in the Hilbert basis with integer coefficients.
Definition
Given a lattice [math]\displaystyle{ L\subset\mathbb{Z}^d }[/math] and a convex polyhedral cone with generators [math]\displaystyle{ a_1,\ldots,a_n\in\mathbb{Z}^d }[/math]
- [math]\displaystyle{ C=\{ \lambda_1 a_1 + \ldots + \lambda_n a_n \mid \lambda_1,\ldots,\lambda_n \geq 0, \lambda_1,\ldots,\lambda_n \in\mathbb{R}\}\subset\mathbb{R}^d, }[/math]
we consider the monoid [math]\displaystyle{ C\cap L }[/math]. By Gordan's lemma, this monoid is finitely generated, i.e., there exists a finite set of lattice points [math]\displaystyle{ \{x_1,\ldots,x_m\}\subset C\cap L }[/math] such that every lattice point [math]\displaystyle{ x\in C\cap L }[/math] is an integer conical combination of these points:
- [math]\displaystyle{ x=\lambda_1 x_1+\ldots+\lambda_m x_m, \quad\lambda_1,\ldots,\lambda_m\in\mathbb{Z}, \lambda_1,\ldots,\lambda_m\geq0. }[/math]
The cone C is called pointed if [math]\displaystyle{ x,-x\in C }[/math] implies [math]\displaystyle{ x=0 }[/math]. In this case there exists a unique minimal generating set of the monoid [math]\displaystyle{ C\cap L }[/math]—the Hilbert basis of C. It is given by the set of irreducible lattice points: An element [math]\displaystyle{ x\in C\cap L }[/math] is called irreducible if it can not be written as the sum of two non-zero elements, i.e., [math]\displaystyle{ x=y+z }[/math] implies [math]\displaystyle{ y=0 }[/math] or [math]\displaystyle{ z=0 }[/math].
References
- Bruns, Winfried; Gubeladze, Joseph; Henk, Martin; Martin, Alexander; Weismantel, Robert (1999), "A counterexample to an integer analogue of Carathéodory's theorem", Journal für die reine und angewandte Mathematik 1999 (510): 179–185, doi:10.1515/crll.1999.045
- Cook, William John; Fonlupt, Jean; Schrijver, Alexander (1986), "An integer analogue of Carathéodory's theorem", Journal of Combinatorial Theory, Series B 40 (1): 63–70, doi:10.1016/0095-8956(86)90064-X
- Eisenbrand, Friedrich; Shmonin, Gennady (2006), "Carathéodory bounds for integer cones", Operations Research Letters 34 (5): 564–568, doi:10.1016/j.orl.2005.09.008, http://infoscience.epfl.ch/record/121640
- D. V. Pasechnik (2001). "On computing the Hilbert bases via the Elliott—MacMahon algorithm". Theoretical Computer Science 263 (1–2): 37–46. doi:10.1016/S0304-3975(00)00229-2.
 |