Graph flattenability
Flattenability in some [math]\displaystyle{ d }[/math]-dimensional normed vector space is a property of graphs which states that any embedding, or drawing, of the graph in some high dimension [math]\displaystyle{ d' }[/math] can be "flattened" down to live in [math]\displaystyle{ d }[/math]-dimensions, such that the distances between pairs of points connected by edges are preserved. A graph [math]\displaystyle{ G }[/math] is [math]\displaystyle{ d }[/math]-flattenable if every distance constraint system (DCS) with [math]\displaystyle{ G }[/math] as its constraint graph has a [math]\displaystyle{ d }[/math]-dimensional framework. Flattenability was first called realizability,[1] but the name was changed to avoid confusion with a graph having some DCS with a [math]\displaystyle{ d }[/math]-dimensional framework.[2] Flattenability has connections to structural rigidity, tensegrities, Cayley configuration spaces, and a variant of the graph realization problem.
Definitions
A distance constraint system [math]\displaystyle{ (G,\delta) }[/math], where [math]\displaystyle{ G=(V,E) }[/math] is a graph and [math]\displaystyle{ \delta: E \rightarrow \mathbb{R}^{|E|} }[/math] is an assignment of distances onto the edges of [math]\displaystyle{ G }[/math], is [math]\displaystyle{ d }[/math]-flattenable in some normed vector space [math]\displaystyle{ \mathbb{R}^d }[/math] if there exists a framework of [math]\displaystyle{ (G,\delta) }[/math] in [math]\displaystyle{ d }[/math]-dimensions.
A graph [math]\displaystyle{ G=(V,E) }[/math] is [math]\displaystyle{ d }[/math]-flattenable in [math]\displaystyle{ \mathbb{R}^d }[/math] if every distance constraint system with [math]\displaystyle{ G }[/math] as its constraint graph is [math]\displaystyle{ d }[/math]-flattenable.
Flattenability can also be defined in terms of Cayley configuration spaces; see connection to Cayley configuration spaces below.
Properties
Closure under subgraphs. Flattenability is closed under taking subgraphs.[1] To see this, observe that for some graph [math]\displaystyle{ G }[/math], all possible embeddings of a subgraph [math]\displaystyle{ H }[/math] of [math]\displaystyle{ G }[/math] are contained in the set of all embeddings of [math]\displaystyle{ G }[/math].
Minor-closed. Flattenability is a minor-closed property by a similar argument as above.[1]
Flattening dimension. The flattening dimension of a graph [math]\displaystyle{ G }[/math] in some normed vector space is the lowest dimension [math]\displaystyle{ d }[/math] such that [math]\displaystyle{ G }[/math] is [math]\displaystyle{ d }[/math]-flattenable. The flattening dimension of a graph is closely related to its gram dimension.[3] The following is an upper-bound on the flattening dimension of an arbitrary graph under the [math]\displaystyle{ l_2 }[/math]-norm.
Theorem. [4] The flattening dimension of a graph [math]\displaystyle{ G = \left(V,E\right) }[/math] under the [math]\displaystyle{ l_2 }[/math]-norm is at most [math]\displaystyle{ O \left( \sqrt{\left| E \right|} \right) }[/math].
For a detailed treatment of this topic, see Chapter 11.2 of Deza & Laurent.[5]
Euclidean flattenability
This section concerns flattenability results in Euclidean space, where distance is measured using the [math]\displaystyle{ l_2 }[/math] norm, also called the Euclidean norm.
1-flattenable graphs
The following theorem is folklore and shows that the only forbidden minor for 1-flattenability is the complete graph [math]\displaystyle{ K_3 }[/math].
Theorem. A graph is 1-flattenable if and only if it is a forest.
Proof. A proof can be found in Belk & Connelly.[1] For one direction, a forest is a collection of trees, and any distance constraint system whose graph is a tree can be realized in 1-dimension. For the other direction, if a graph [math]\displaystyle{ G }[/math] is not a forest, then it has the complete graph [math]\displaystyle{ K_3 }[/math] as a subgraph. Consider the DCS that assigns the distance 1 to the edges of the [math]\displaystyle{ K_4 }[/math] subgraph and the distance 0 to all other edges. This DCS has a realization in 2-dimensions as the 1-skeleton of a triangle, but it has no realization in 1-dimension.
This proof allowed for distances on edges to be 0, but the argument holds even when this is not allowed. See Belk & Connelly[1] for a detailed explanation.
2-flattenable graphs
The following theorem is folklore and shows that the only forbidden minor for 2-flattenability is the complete graph [math]\displaystyle{ K_4 }[/math].
Theorem. A graph is 2-flattenable if and only if it is a partial 2-tree.
Proof. A proof can be found in Belk & Connelly.[1] For one direction, since flattenability is closed under taking subgraphs, it is sufficient to show that 2-trees are 2-flattenable. A 2-tree with [math]\displaystyle{ n }[/math] vertices can be constructed recursively by taking a 2-tree with [math]\displaystyle{ n-1 }[/math] vertices and connecting a new vertex to the vertices of an existing edge. The base case is the [math]\displaystyle{ K_3 }[/math]. Proceed by induction on the number of vertices [math]\displaystyle{ n }[/math]. When [math]\displaystyle{ n=3 }[/math], consider any distance assignment [math]\displaystyle{ \delta }[/math] on the edges [math]\displaystyle{ K_3 }[/math]. Note that if [math]\displaystyle{ \delta }[/math] does not obey the triangle inequality, then this DCS does not have a realization in any dimension. Without loss of generality, place the first vertex [math]\displaystyle{ v_1 }[/math] at the origin and the second vertex [math]\displaystyle{ v_2 }[/math] along the x-axis such that [math]\displaystyle{ \delta_{12} }[/math] is satisfied. The third vertex [math]\displaystyle{ v_3 }[/math] can be placed at an intersection of the circles with centers [math]\displaystyle{ v_1 }[/math] and [math]\displaystyle{ v_2 }[/math] and radii [math]\displaystyle{ \delta_{13} }[/math] and [math]\displaystyle{ \delta_{23} }[/math] respectively. This method of placement is called a ruler and compass construction. Hence, [math]\displaystyle{ K_3 }[/math] is 2-flattenable.
Now, assume a 2-tree with [math]\displaystyle{ k }[/math] vertices is 2-flattenable. By definition, a 2-tree with [math]\displaystyle{ k+1 }[/math] vertices is a 2-tree with [math]\displaystyle{ k }[/math] vertices, say [math]\displaystyle{ T }[/math], and an additional vertex [math]\displaystyle{ u }[/math] connected to the vertices of an existing edge in [math]\displaystyle{ T }[/math]. By the inductive hypothesis, [math]\displaystyle{ T }[/math] is 2-flattenable. Finally, by a similar ruler and compass construction argument as in the base case, [math]\displaystyle{ u }[/math] can be placed such that it lies in the plane. Thus, 2-trees are 2-flattenable by induction.
If a graph [math]\displaystyle{ G }[/math] is not a partial 2-tree, then it contains [math]\displaystyle{ K_4 }[/math] as a minor. Assigning the distance of 1 to the edges of the [math]\displaystyle{ K_4 }[/math] minor and the distance of 0 to all other edges yields a DCS with a realization in 3-dimensions as the 1-skeleton of a tetrahedra. However, this DCS has no realization in 2-dimensions: when attempting to place the fourth vertex using a ruler and compass construction, the three circles defined by the fourth vertex do not all intersect.
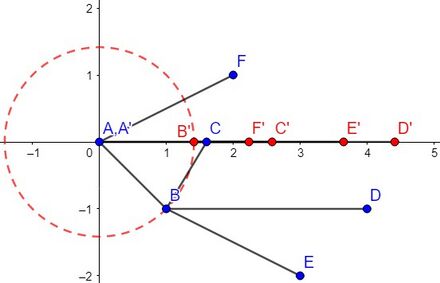
Example. Consider the graph in figure 2. Adding the edge [math]\displaystyle{ \bar{AC} }[/math] turns it into a 2-tree; hence, it is a partial 2-tree. Thus, it is 2-flattenable.
Example. The wheel graph [math]\displaystyle{ W_5 }[/math] contains [math]\displaystyle{ K_4 }[/math] as a minor. Thus, it is not 2-flattenable.
3-flattenable graphs
The class of 3-flattenable graphs strictly contains the class of partial 3-trees.[1] More precisely, the forbidden minors for partial 3-trees are the complete graph [math]\displaystyle{ K_5 }[/math], the 1-skeleton of the octahedron [math]\displaystyle{ K_{2,2,2} }[/math], [math]\displaystyle{ V_8 }[/math], and [math]\displaystyle{ C_5 \times C_2 }[/math], but [math]\displaystyle{ V_8 }[/math], and [math]\displaystyle{ C_5 \times C_2 }[/math] are 3-flattenable.[6] These graphs are shown in Figure 3. Furthermore, the following theorem from Belk & Connelly[1] shows that the only forbidden minors for 3-flattenability are [math]\displaystyle{ K_5 }[/math] and [math]\displaystyle{ K_{2,2,2} }[/math].
Theorem. [1] A graph is 3-flattenable if and only if it does not have [math]\displaystyle{ K_5 }[/math] or [math]\displaystyle{ K_{2,2,2} }[/math] as a minor.
Proof Idea: The proof given in Belk & Connelly[1] assumes that [math]\displaystyle{ V_8 }[/math], and [math]\displaystyle{ C_5 \times C_2 }[/math] are 3-realizable. This is proven in the same article using mathematical tools from rigidity theory, specifically those concerning tensegrities. The complete graph [math]\displaystyle{ K_5 }[/math] is not 3-flattenable, and the same argument that shows [math]\displaystyle{ K_4 }[/math] is not 2-flattenable and [math]\displaystyle{ K_3 }[/math] is not 1-flattenable works here: assigning the distance 1 to the edges of [math]\displaystyle{ K_5 }[/math] yields a DCS with no realization in 3-dimensions. Figure 4 gives a visual proof that the graph [math]\displaystyle{ K_{2,2,2} }[/math] is not 3-flattenable. Vertices 1, 2, and 3 form a degenerate triangle. For the edges between vertices 1- 5, edges [math]\displaystyle{ (1,4) }[/math] and [math]\displaystyle{ (3,4) }[/math] are assigned the distance [math]\displaystyle{ \sqrt{2} }[/math] and all other edges are assigned the distance 1. Vertices 1- 5 have unique placements in 3-dimensions, up to congruence. Vertex 6 has 2 possible placements in 3-dimensions: 1 on each side of the plane [math]\displaystyle{ \Pi }[/math] defined by vertices 1, 2, and 4. Hence, the edge [math]\displaystyle{ (5,6) }[/math] has two distance values that can be realized in 3-dimensions. However, vertex 6 can revolve around the plane [math]\displaystyle{ \Pi }[/math] in 4-dimensions while satisfying all constraints, so the edge [math]\displaystyle{ (5,6) }[/math] has infinitely many distance values that can only be realized in 4-dimensions or higher. Thus, [math]\displaystyle{ K_{2,2,2} }[/math] is not 3-flattenable. The fact that these graphs are not 3-flattenable proves that any graph with either [math]\displaystyle{ K_5 }[/math] or [math]\displaystyle{ K_{2,2,2} }[/math] as a minor is not 3-flattenable.

The other direction shows that if a graph [math]\displaystyle{ G }[/math] does not have [math]\displaystyle{ K_5 }[/math] or [math]\displaystyle{ K_{2,2,2} }[/math] as a minor, then [math]\displaystyle{ G }[/math] can be constructed from partial 3-trees, [math]\displaystyle{ V_8 }[/math], and [math]\displaystyle{ C_5 \times C_2 }[/math] via 1-sums, 2-sums, and 3-sums. These graphs are all 3-flattenable and these operations preserve 3-flattenability, so [math]\displaystyle{ G }[/math] is 3-flattenable.
The techniques in this proof yield the following result from Belk & Connelly.[1]
Theorem. [1] Every 3-realizable graph is a subgraph of a graph that can be obtained by a sequence of 1-sums, 2-sums, and 3-sums of the graphs [math]\displaystyle{ K_4 }[/math], [math]\displaystyle{ V_8 }[/math], and [math]\displaystyle{ C_5 \times C_2 }[/math].
Example. The previous theorem can be applied to show that the 1-skeleton of a cube is 3-flattenable. Start with the graph [math]\displaystyle{ K_4 }[/math], which is the 1-skeleton of a tetrahedron. On each face of the tetrahedron, perform a 3-sum with another [math]\displaystyle{ K_4 }[/math] graph, i.e. glue two tetrahedra together on their faces. The resulting graph contains the cube as a subgraph and is 3-flattenable.
In higher dimensions
Giving a forbidden minor characterization of [math]\displaystyle{ d }[/math]-flattenable graphs, for dimension [math]\displaystyle{ d\gt 3 }[/math], is an open problem. For any dimension [math]\displaystyle{ d }[/math], [math]\displaystyle{ K_{d+2} }[/math] and the 1-skeleton of the [math]\displaystyle{ d }[/math]-dimensional analogue of an octahedron are forbidden minors for [math]\displaystyle{ d }[/math]-flattenability.[1] It is conjectured that the number of forbidden minors for [math]\displaystyle{ d }[/math]-flattenability grows asymptotically to the number of forbidden minors for partial [math]\displaystyle{ d }[/math]-trees, and there are over [math]\displaystyle{ 75 }[/math] forbidden minors for partial 4-trees.[1]
An alternative characterization of [math]\displaystyle{ d }[/math]-flattenable graphs relates flattenability to Cayley configuration spaces.[2][7] See the section on the connection to Cayley configuration spaces.
Connection to the graph realization problem
Given a distance constraint system and a dimension [math]\displaystyle{ d }[/math], the graph realization problem asks for a [math]\displaystyle{ d }[/math]-dimensional framework of the DCS, if one exists. There are algorithms to realize [math]\displaystyle{ d }[/math]-flattenable graphs in [math]\displaystyle{ d }[/math]-dimensions, for [math]\displaystyle{ d \leq 3 }[/math], that run in polynomial time in the size of the graph. For [math]\displaystyle{ d=1 }[/math], realizing each tree in a forest in 1-dimension is trivial to accomplish in polynomial time. An algorithm for [math]\displaystyle{ d=2 }[/math] is mentioned in Belk & Connelly.[1] For [math]\displaystyle{ d=3 }[/math], the algorithm in So & Ye[8] obtains a framework [math]\displaystyle{ r }[/math] of a DCS using semidefinite programming techniques and then utilizes the "folding" method described in Belk[6] to transform [math]\displaystyle{ r }[/math] into a 3-dimensional framework.
Flattenability under p-norms
This section concerns flattenability results for graphs under general [math]\displaystyle{ p }[/math]-norms, for [math]\displaystyle{ 1 \leq p \leq \infty }[/math].
Connection to algebraic geometry
Determining the flattenability of a graph under a general [math]\displaystyle{ p }[/math]-norm can be accomplished using methods in algebraic geometry, as suggested in Belk & Connelly.[1] The question of whether a graph [math]\displaystyle{ G=(V,E) }[/math] is [math]\displaystyle{ d }[/math]-flattenable is equivalent to determining if two semi-algebraic sets are equal. One algorithm to compare two semi-algebraic sets takes [math]\displaystyle{ (4|E|)^{O\left(nd|V|^2\right)} }[/math] time.[9]
Connection to Cayley configuration spaces
For general [math]\displaystyle{ l_p }[/math]-norms, there is a close relationship between flattenability and Cayley configuration spaces.[2][7] The following theorem and its corollary are found in Sitharam & Willoughby.[2]
Theorem. [2] A graph [math]\displaystyle{ G }[/math] is [math]\displaystyle{ d }[/math]-flattenable if and only if for every subgraph [math]\displaystyle{ H=G \setminus F }[/math] of [math]\displaystyle{ G }[/math] resulting from removing a set of edges [math]\displaystyle{ F }[/math] from [math]\displaystyle{ G }[/math] and any [math]\displaystyle{ l^p_p }[/math]-distance vector [math]\displaystyle{ \delta_H }[/math] such that the DCS [math]\displaystyle{ (H,\delta_H) }[/math] has a realization, the [math]\displaystyle{ d }[/math]-dimensional Cayley configuration space of [math]\displaystyle{ (H,\delta_H) }[/math] over [math]\displaystyle{ F }[/math] is convex.
Corollary. A graph [math]\displaystyle{ G }[/math] is not [math]\displaystyle{ d }[/math]-flattenable if there exists some subgraph [math]\displaystyle{ H=G \setminus F }[/math] of [math]\displaystyle{ G }[/math] and some [math]\displaystyle{ l^p_p }[/math]-distance vector [math]\displaystyle{ \delta }[/math] such that the [math]\displaystyle{ d }[/math]-dimensional Cayley configuration space of [math]\displaystyle{ (H,\delta_H) }[/math] over [math]\displaystyle{ F }[/math] is not convex.
2-Flattenability under the l1 and l∞ norms
The [math]\displaystyle{ l_1 }[/math] and [math]\displaystyle{ l_{\infty} }[/math] norms are equivalent up to rotating axes in 2-dimensions,[5] so 2-flattenability results for either norm hold for both. This section uses the [math]\displaystyle{ l_1 }[/math]-norm. The complete graph [math]\displaystyle{ K_4 }[/math] is 2-flattenable under the [math]\displaystyle{ l_1 }[/math]-norm and [math]\displaystyle{ K_5 }[/math] is 3-flattenable, but not 2-flattenable.[10] These facts contribute to the following results on 2-flattenability under the [math]\displaystyle{ l_1 }[/math]-norm found in Sitharam & Willoughby.[2]
Observation. [2] The set of 2-flattenable graphs under the [math]\displaystyle{ l_1 }[/math]-norm (and [math]\displaystyle{ l_{\infty} }[/math]-norm) strictly contains the set of 2-flattenable graphs under the [math]\displaystyle{ l_2 }[/math]-norm.
Theorem. [2] A 2-sum of 2-flattenable graphs is 2-flattenable if and only if at most one graph has a [math]\displaystyle{ K_4 }[/math] minor.
The fact that [math]\displaystyle{ K_4 }[/math] is 2-flattenable but [math]\displaystyle{ K_5 }[/math] is not has implications on the forbidden minor characterization for 2-flattenable graphs under the [math]\displaystyle{ l_1 }[/math]-norm. Specifically, the minors of [math]\displaystyle{ K_5 }[/math] could be forbidden minors for 2-flattenability. The following results explore these possibilities and give the complete set of forbidden minors.
Theorem. [2] The banana graph, or [math]\displaystyle{ K_5 }[/math] with one edge removed, is not 2-flattenable.
Observation. [2] The graph obtained by removing two edges that are incident to the same vertex from [math]\displaystyle{ K_5 }[/math] is 2-flattenable.
Observation. [2] Connected graphs on 5 vertices with 7 edges are 2-flattenable.
The only minor of [math]\displaystyle{ K_5 }[/math] left is the wheel graph [math]\displaystyle{ W_5 }[/math], and the following result shows that this is one of the forbidden minors.
Theorem. [11] A graph is 2-flattenable under the [math]\displaystyle{ l_1 }[/math]- or [math]\displaystyle{ l_{\infty} }[/math]-norm if and only if it does not have either of the following graphs as minors:
- the wheel graph [math]\displaystyle{ W_5 }[/math] or
- the graph obtained by taking the 2-sum of two copies of [math]\displaystyle{ K_4 }[/math] and removing the shared edge.
Connection to structural rigidity
This section relates flattenability to concepts in structural (combinatorial) rigidity theory, such as the rigidity matroid. The following results concern the [math]\displaystyle{ l^p_p }[/math]-distance cone [math]\displaystyle{ \Phi_{n,l_p} }[/math], i.e., the set of all [math]\displaystyle{ l^p_p }[/math]-distance vectors that can be realized as a configuration of [math]\displaystyle{ n }[/math] points in some dimension. A proof that this set is a cone can be found in Ball.[12] The [math]\displaystyle{ d }[/math]-stratum of this cone [math]\displaystyle{ \Phi^d_{n,l_p} }[/math] are the vectors that can be realized as a configuration of [math]\displaystyle{ n }[/math] points in [math]\displaystyle{ d }[/math]-dimensions. The projection of [math]\displaystyle{ \Phi_{n,l_p} }[/math] or [math]\displaystyle{ \Phi^d_{n,l_p} }[/math] onto the edges of a graph [math]\displaystyle{ G }[/math] is the set of [math]\displaystyle{ l^p_p }[/math] distance vectors that can be realized as the edge-lengths of some embedding of [math]\displaystyle{ G }[/math].
A generic property of a graph [math]\displaystyle{ G }[/math] is one that almost all frameworks of distance constraint systems, whose graph is [math]\displaystyle{ G }[/math], have. A framework of a DCS [math]\displaystyle{ (G,\delta) }[/math] under an [math]\displaystyle{ l_p }[/math]-norm is a generic framework (with respect to [math]\displaystyle{ d }[/math]-flattenability) if the following two conditions hold:
- there is an open neighborhood [math]\displaystyle{ \Omega }[/math] of [math]\displaystyle{ \delta }[/math] in the interior of the cone [math]\displaystyle{ \Phi_{n,l_p} }[/math], and
- the framework is [math]\displaystyle{ d }[/math]-flattenable if and only if all frameworks in [math]\displaystyle{ \Omega }[/math] are [math]\displaystyle{ d }[/math]-flattenable.
Condition (1) ensures that the neighborhood [math]\displaystyle{ \Omega }[/math] has full rank. In other words, [math]\displaystyle{ \Omega }[/math] has dimension equal to the flattening dimension of the complete graph [math]\displaystyle{ K_n }[/math] under the [math]\displaystyle{ l_p }[/math]-norm. See Kitson[13] for a more detailed discussion of generic framework for [math]\displaystyle{ l_p }[/math]-norms. The following results are found in Sitharam & Willoughby.[2]
Theorem. [2] A graph [math]\displaystyle{ G }[/math] is [math]\displaystyle{ d }[/math]-flattenable if and only if every generic framework of [math]\displaystyle{ G }[/math] is [math]\displaystyle{ d }[/math]-flattenable.
Theorem. [2] [math]\displaystyle{ d }[/math]-flattenability is not a generic property of graphs, even for the [math]\displaystyle{ l_2 }[/math]-norm.
Theorem. [2] A generic [math]\displaystyle{ d }[/math]-flattenable framework of a graph [math]\displaystyle{ G }[/math] exists if and only if [math]\displaystyle{ G }[/math] is independent in the generic [math]\displaystyle{ d }[/math]-dimensional rigidity matroid.
Corollary. [2] A graph [math]\displaystyle{ G }[/math] is [math]\displaystyle{ d }[/math]-flattenable only if [math]\displaystyle{ G }[/math] is independent in the [math]\displaystyle{ d }[/math]-dimensional rigidity matroid.
Theorem. [2] For general [math]\displaystyle{ l_p }[/math]-norms, a graph [math]\displaystyle{ G }[/math] is
- independent in the generic [math]\displaystyle{ d }[/math]-dimensional rigidity matroid if and only if the projection of the [math]\displaystyle{ d }[/math]-stratum [math]\displaystyle{ \Phi^d_{n,l_p} }[/math] onto the edges of [math]\displaystyle{ G }[/math] has dimension equal to the number of edges of [math]\displaystyle{ G }[/math];
- maximally independent in the generic [math]\displaystyle{ d }[/math]-dimensional rigidity matroid if and only if projecting the [math]\displaystyle{ d }[/math]-stratum [math]\displaystyle{ \Phi^d_{n,l_p} }[/math] onto the edges of [math]\displaystyle{ G }[/math] preserves its dimension and this dimension is equal to the number of edges of [math]\displaystyle{ G }[/math];
- rigid in [math]\displaystyle{ d }[/math]-dimensions if and only if projecting the [math]\displaystyle{ d }[/math]-stratum [math]\displaystyle{ \Phi^d_{n,l_p} }[/math] onto the edges of [math]\displaystyle{ G }[/math] preserves its dimension;
- not independent in the generic [math]\displaystyle{ d }[/math]-dimensional rigidity matroid if and only if the dimension of the projection of the [math]\displaystyle{ d }[/math]-stratum [math]\displaystyle{ \Phi^d_{n,l_p} }[/math] onto the edges of [math]\displaystyle{ G }[/math] is strictly less than the minimum of the dimension of [math]\displaystyle{ \Phi^d_{n,l_p} }[/math] and the number of edges of [math]\displaystyle{ G }[/math].
References
- ↑ 1.00 1.01 1.02 1.03 1.04 1.05 1.06 1.07 1.08 1.09 1.10 1.11 1.12 1.13 1.14 1.15 1.16 Belk, Maria; Connelly, Robert (2007). "Realizability of Graphs". Discrete & Computational Geometry 37 (2): 125–137. doi:10.1007/s00454-006-1284-5.
- ↑ 2.00 2.01 2.02 2.03 2.04 2.05 2.06 2.07 2.08 2.09 2.10 2.11 2.12 2.13 2.14 2.15 2.16 Sitharam, M.; Willoughby, J. (2014). "On Flattenability of Graphs". Automated Deduction in Geometry. Lecture Notes in Computer Science 9201: 129–148. doi:10.1007/978-3-319-21362-0_9. ISBN 978-3-319-21361-3.
- ↑ Laurent, Monique; Varvitsiotis, Antonios (2012). "The Gram Dimension of a Graph". Combinatorial Optimization. Lecture Notes in Computer Science. 7422. pp. 356–367. doi:10.1007/978-3-642-32147-4_32. ISBN 978-3-642-32146-7.
- ↑ Barvinok, A. (1995). "Problems of distance geometry and convex properties of quadratic maps". Discrete & Computational Geometry 13 (2): 189–202. doi:10.1007/BF02574037.
- ↑ 5.0 5.1 Deza, Michel; Laurent, Monique (1997). Geometry of Cuts and Metrics. Springer-Verlag Berlin Heidelberg. doi:10.1007/978-3-642-04295-9. ISBN 978-3-540-61611-5.
- ↑ 6.0 6.1 Belk, Maria (2007). "Realizability of Graphs in Three Dimensions". Discrete & Computational Geometry 37 (2): 139–162. doi:10.1007/s00454-006-1285-4.
- ↑ 7.0 7.1 Sitharam, Meera; Gao, Heping (2010). "Characterizing Graphs with Convex and Connected Cayley Configuration Spaces". Discrete & Computational Geometry 43 (3): 594–625. doi:10.1007/s00454-009-9160-8.
- ↑ So, Anthony Man-Cho; Ye, Yinyu (2006). "A semidefinite programming approach to tensegrity theory and realizability of graphs". Proceedings of the seventeenth annual ACM-SIAM symposium on Discrete algorithm - SODA '06. pp. 766–775. doi:10.1145/1109557.1109641. ISBN 0898716055.
- ↑ Basu, Saugata; Pollack, Richard; Marie-Francoise, Roy (2003). "Existential Theory of the Reals". Algorithms in Real Algebraic Geometry. Algorithms and Computation in Mathematics. 10. Springer, Berlin, Heidelberg. doi:10.1007/3-540-33099-2_14. ISBN 978-3-540-33098-1.
- ↑ Witsenhausen, Hans S. (1986). "Minimum dimension embedding of finite metric spaces". Journal of Combinatorial Theory. Series A 42 (2): 184–199. doi:10.1016/0097-3165(86)90089-0.
- ↑ Fiorini, Samuel; Huynh, Tony; Joret, Gwenaël; Varvitsiotis, Antonios (2017-01-01). "The Excluded Minors for Isometric Realizability in the Plane". SIAM Journal on Discrete Mathematics 31 (1): 438–453. doi:10.1137/16M1064775. ISSN 0895-4801. https://epubs.siam.org/doi/10.1137/16M1064775.
- ↑ Ball, Keith (1990). "Isometric Embedding in lp-spaces". European Journal of Combinatorics 11 (4): 305–311. doi:10.1016/S0195-6698(13)80131-X.
- ↑ Kitson, Derek (2015). "Finite and Infinitesimal Rigidity with Polyhedral Norms". Discrete & Computational Geometry 54 (2): 390–411. doi:10.1007/s00454-015-9706-x.
 |