Flattening
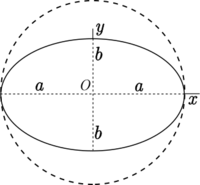
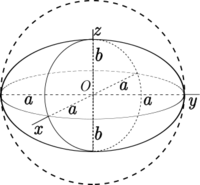
Flattening is a measure of the compression of a circle or sphere along a diameter to form an ellipse or an ellipsoid of revolution (spheroid) respectively. Other terms used are ellipticity, or oblateness. The usual notation for flattening is [math]\displaystyle{ f }[/math] and its definition in terms of the semi-axes [math]\displaystyle{ a }[/math] and [math]\displaystyle{ b }[/math] of the resulting ellipse or ellipsoid is
- [math]\displaystyle{ f =\frac {a - b}{a}. }[/math]
The compression factor is [math]\displaystyle{ b/a }[/math] in each case; for the ellipse, this is also its aspect ratio.
Definitions
There are three variants: the flattening [math]\displaystyle{ f, }[/math][1] sometimes called the first flattening,[2] as well as two other "flattenings" [math]\displaystyle{ f' }[/math] and [math]\displaystyle{ n, }[/math] each sometimes called the second flattening,[3] sometimes only given a symbol,[4] or sometimes called the second flattening and third flattening, respectively.[5]
In the following, [math]\displaystyle{ a }[/math] is the larger dimension (e.g. semimajor axis), whereas [math]\displaystyle{ b }[/math] is the smaller (semiminor axis). All flattenings are zero for a circle (a = b).
(First) flattening [math]\displaystyle{ f }[/math] [math]\displaystyle{ \frac{a-b}{a} }[/math] Fundamental. Geodetic reference ellipsoids are specified by giving [math]\displaystyle{ \frac{1}{f}\,\! }[/math] Second flattening [math]\displaystyle{ f' }[/math] [math]\displaystyle{ \frac{a-b}{b} }[/math] Rarely used. Third flattening [math]\displaystyle{ n }[/math] [math]\displaystyle{ \frac{a-b}{a+b} }[/math] Used in geodetic calculations as a small expansion parameter.[6]
Identities
The flattenings can be related to each-other:
- [math]\displaystyle{ \begin{align} f = \frac{2n}{1 + n}, \\[5mu] n = \frac{f}{2 - f}. \end{align} }[/math]
The flattenings are related to other parameters of the ellipse. For example,
- [math]\displaystyle{ \begin{align} \frac ba &= 1-f = \frac{1-n}{1+n}, \\[5mu] e^2 &= 2f-f^2 = \frac{4n}{(1+n)^2}, \\[5mu] f &= 1-\sqrt{1-e^2}, \end{align} }[/math]
where [math]\displaystyle{ e }[/math] is the eccentricity.
See also
- Earth flattening
- Eccentricity (mathematics) § Ellipses
- Equatorial bulge
- Ovality
- Planetary flattening
- Sphericity
- Roundness (object)
References
- ↑ Snyder, John P. (1987). Map Projections: A Working Manual. U.S. Geological Survey Professional Paper. 1395. Washington, D.C.: U.S. Government Printing Office. doi:10.3133/pp1395. https://pubs.er.usgs.gov/publication/pp1395.
- ↑ Tenzer, Róbert (2002). "Transformation of the Geodetic Horizontal Control to Another Reference Ellipsoid". Studia Geophysica et Geodaetica 46 (1): 27–32. doi:10.1023/A:1019881431482. ProQuest 750849329. https://www.proquest.com/docview/750849329.
- ↑ For example, [math]\displaystyle{ f' }[/math] is called the second flattening in: Template:Cite tech report However, [math]\displaystyle{ n }[/math] is called the second flattening in: Hooijberg, Maarten (1997). Practical Geodesy: Using Computers. Springer. p. 41. doi:10.1007/978-3-642-60584-0_3.
- ↑ Maling, Derek Hylton (1992). Coordinate Systems and Map Projections (2nd ed.). Oxford; New York: Pergamon Press. p. 65. ISBN 0-08-037233-3. Template:Cite tech report Osborne, P. (2008). "The Mercator Projections". §5.2. http://mercator.myzen.co.uk/mercator.pdf.
- ↑ Lapaine, Miljenko (2017). "Basics of Geodesy for Map Projections". in Lapaine, Miljenko; Usery, E. Lynn. Choosing a Map Projection. Lecture Notes in Geoinformation and Cartography. pp. 327–343. doi:10.1007/978-3-319-51835-0_13. ISBN 978-3-319-51834-3.Karney, Charles F.F. (2023). "On auxiliary latitudes". Survey Review: 1–16. doi:10.1080/00396265.2023.2217604.
- ↑ F. W. Bessel, 1825, Uber die Berechnung der geographischen Langen und Breiten aus geodatischen Vermessungen, Astron.Nachr., 4(86), 241–254, doi:10.1002/asna.201011352, translated into English by C. F. F. Karney and R. E. Deakin as The calculation of longitude and latitude from geodesic measurements, Astron. Nachr. 331(8), 852–861 (2010), E-print arXiv:0908.1824, Bibcode: 1825AN......4..241B
 |