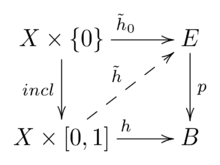Fibration
The notion of a fibration generalizes the notion of a fiber bundle and plays an important role in algebraic topology, a branch of mathematics.
Fibrations are used, for example, in Postnikov systems or obstruction theory.
In this article, all mappings are continuous mappings between topological spaces.
Formal definitions
Homotopy lifting property
A mapping [math]\displaystyle{ p \colon E \to B }[/math] satisfies the homotopy lifting property for a space [math]\displaystyle{ X }[/math] if:
- for every homotopy [math]\displaystyle{ h \colon X \times [0, 1] \to B }[/math] and
- for every mapping (also called lift) [math]\displaystyle{ \tilde h_0 \colon X \to E }[/math] lifting [math]\displaystyle{ h|_{X \times 0} = h_0 }[/math] (i.e. [math]\displaystyle{ h_0 = p \circ \tilde h_0 }[/math])
there exists a (not necessarily unique) homotopy [math]\displaystyle{ \tilde h \colon X \times [0, 1] \to E }[/math] lifting [math]\displaystyle{ h }[/math] (i.e. [math]\displaystyle{ h = p \circ \tilde h }[/math]) with [math]\displaystyle{ \tilde h_0 = \tilde h|_{X \times 0}. }[/math]
The following commutative diagram shows the situation: [1]:66
Fibration
A fibration (also called Hurewicz fibration) is a mapping [math]\displaystyle{ p \colon E \to B }[/math] satisfying the homotopy lifting property for all spaces [math]\displaystyle{ X. }[/math] The space [math]\displaystyle{ B }[/math] is called base space and the space [math]\displaystyle{ E }[/math] is called total space. The fiber over [math]\displaystyle{ b \in B }[/math] is the subspace [math]\displaystyle{ F_b = p^{-1}(b) \subseteq E. }[/math][1]:66
Serre fibration
A Serre fibration (also called weak fibration) is a mapping [math]\displaystyle{ p \colon E \to B }[/math] satisfying the homotopy lifting property for all CW-complexes.[2]:375-376
Every Hurewicz fibration is a Serre fibration.
Quasifibration
A mapping [math]\displaystyle{ p \colon E \to B }[/math] is called quasifibration, if for every [math]\displaystyle{ b \in B, }[/math] [math]\displaystyle{ e \in p^{-1}(b) }[/math] and [math]\displaystyle{ i \geq 0 }[/math] holds that the induced mapping [math]\displaystyle{ p_* \colon \pi_i(E, p^{-1}(b), e) \to \pi_i(B, b) }[/math] is an isomorphism.
Every Serre fibration is a quasifibration.[3]:241-242
Examples
- The projection onto the first factor [math]\displaystyle{ p \colon B \times F \to B }[/math] is a fibration. That is, trivial bundles are fibrations.
- Every covering [math]\displaystyle{ p \colon E \to B }[/math] is a fibration. Specifically, for every homotopy [math]\displaystyle{ h \colon X \times [0, 1] \to B }[/math] and every lift [math]\displaystyle{ \tilde h_0 \colon X \to E }[/math] there exists a uniquely defined lift [math]\displaystyle{ \tilde h \colon X \times [0,1] \to E }[/math] with [math]\displaystyle{ p \circ \tilde h = h. }[/math][4]:159 [5]:50
- Every fiber bundle [math]\displaystyle{ p \colon E \to B }[/math] satisfies the homotopy lifting property for every CW-complex.[2]:379
- A fiber bundle with a paracompact and Hausdorff base space satisfies the homotopy lifting property for all spaces.[2]:379
- An example for a fibration, which is not a fiber bundle, is given by the mapping [math]\displaystyle{ i^* \colon X^{I^k} \to X^{\partial I^k} }[/math] induced by the inclusion [math]\displaystyle{ i \colon \partial I^k \to I^k }[/math] where [math]\displaystyle{ k \in \N, }[/math] [math]\displaystyle{ X }[/math] a topological space and [math]\displaystyle{ X^{A} = \{f \colon A \to X\} }[/math] is the space of all continuous mappings with the compact-open topology.[4]:198
- The Hopf fibration [math]\displaystyle{ S^1 \to S^3 \to S^2 }[/math] is a non trivial fiber bundle and specifically a Serre fibration.
Basic concepts
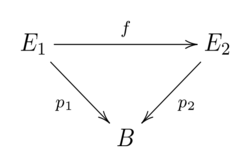
Fiber homotopy equivalence
A mapping [math]\displaystyle{ f \colon E_1 \to E_2 }[/math] between total spaces of two fibrations [math]\displaystyle{ p_1 \colon E_1 \to B }[/math] and [math]\displaystyle{ p_2 \colon E_2 \to B }[/math] with the same base space is a fibration homomorphism if the following diagram commutes:
The mapping [math]\displaystyle{ f }[/math] is a fiber homotopy equivalence if in addition a fibration homomorphism [math]\displaystyle{ g \colon E_2 \to E_1 }[/math] exists, such that the mappings [math]\displaystyle{ f \circ g }[/math] and [math]\displaystyle{ g \circ f }[/math] are homotopic, by fibration homomorphisms, to the identities [math]\displaystyle{ Id_{E_2} }[/math] and [math]\displaystyle{ Id_{E_1}. }[/math] [2]:405-406
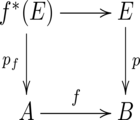
Pullback fibration
Given a fibration [math]\displaystyle{ p \colon E \to B }[/math] and a mapping [math]\displaystyle{ f \colon A \to B }[/math], the mapping [math]\displaystyle{ p_f \colon f^*(E) \to A }[/math] is a fibration, where [math]\displaystyle{ f^*(E) = \{(a, e) \in A \times E | f(a) = p(e)\} }[/math] is the pullback and the projections of [math]\displaystyle{ f^*(E) }[/math] onto [math]\displaystyle{ A }[/math] and [math]\displaystyle{ E }[/math] yield the following commutative diagram:
The fibration [math]\displaystyle{ p_f }[/math] is called the pullback fibration or induced fibration.[2]:405-406
Pathspace fibration
With the pathspace construction, any continuous mapping can be extended to a fibration by enlarging its domain to a homotopy equivalent space. This fibration is called pathspace fibration.
The total space [math]\displaystyle{ E_f }[/math] of the pathspace fibration for a continuous mapping [math]\displaystyle{ f \colon A \to B }[/math] between topological spaces consists of pairs [math]\displaystyle{ (a, \gamma) }[/math] with [math]\displaystyle{ a \in A }[/math] and paths [math]\displaystyle{ \gamma \colon I \to B }[/math] with starting point [math]\displaystyle{ \gamma (0) = f(a), }[/math] where [math]\displaystyle{ I = [0, 1] }[/math] is the unit interval. The space [math]\displaystyle{ E_f = \{ (a, \gamma) \in A \times B^I | \gamma (0) = f(a) \} }[/math] carries the subspace topology of [math]\displaystyle{ A \times B^I, }[/math] where [math]\displaystyle{ B^I }[/math] describes the space of all mappings [math]\displaystyle{ I \to B }[/math] and carries the compact-open topology.
The pathspace fibration is given by the mapping [math]\displaystyle{ p \colon E_f \to B }[/math] with [math]\displaystyle{ p(a, \gamma) = \gamma (1). }[/math] The fiber [math]\displaystyle{ F_f }[/math] is also called the homotopy fiber of [math]\displaystyle{ f }[/math] and consists of the pairs [math]\displaystyle{ (a, \gamma) }[/math] with [math]\displaystyle{ a \in A }[/math] and paths [math]\displaystyle{ \gamma \colon [0, 1] \to B, }[/math] where [math]\displaystyle{ \gamma(0) = f(a) }[/math] and [math]\displaystyle{ \gamma(1) = b_0 \in B }[/math] holds.
For the special case of the inclusion of the base point [math]\displaystyle{ i \colon b_0 \to B }[/math], an important example of the pathspace fibration emerges. The total space [math]\displaystyle{ E_i }[/math] consists of all paths in [math]\displaystyle{ B }[/math] which starts at [math]\displaystyle{ b_0. }[/math] This space is denoted by [math]\displaystyle{ PB }[/math] and is called path space. The pathspace fibration [math]\displaystyle{ p \colon PB \to B }[/math] maps each path to its endpoint, hence the fiber [math]\displaystyle{ p^{-1}(b_0) }[/math] consists of all closed paths. The fiber is denoted by [math]\displaystyle{ \Omega B }[/math] and is called loop space.[2]:407-408
Properties
- The fibers [math]\displaystyle{ p^{-1}(b) }[/math] over [math]\displaystyle{ b \in B }[/math] are homotopy equivalent for each path component of [math]\displaystyle{ B. }[/math][2]:405
- For a homotopy [math]\displaystyle{ f \colon [0, 1] \times A \to B }[/math] the pullback fibrations [math]\displaystyle{ f^*_0(E) \to A }[/math] and [math]\displaystyle{ f^*_1(E) \to A }[/math] are fiber homotopy equivalent.[2]:406
- If the base space [math]\displaystyle{ B }[/math] is contractible, then the fibration [math]\displaystyle{ p \colon E \to B }[/math] is fiber homotopy equivalent to the product fibration [math]\displaystyle{ B \times F \to B. }[/math][2]:406
- The pathspace fibration of a fibration [math]\displaystyle{ p \colon E \to B }[/math] is very similar to itself. More precisely, the inclusion [math]\displaystyle{ E \hookrightarrow E_p }[/math] is a fiber homotopy equivalence.[2]:408
- For a fibration [math]\displaystyle{ p \colon E \to B }[/math] with fiber [math]\displaystyle{ F }[/math] and contractible total space, there is a weak homotopy equivalence [math]\displaystyle{ F \to \Omega B. }[/math][2]:408
Puppe sequence
For a fibration [math]\displaystyle{ p \colon E \to B }[/math] with fiber [math]\displaystyle{ F }[/math] and base point [math]\displaystyle{ b_0 \in B }[/math] the inclusion [math]\displaystyle{ F \hookrightarrow F_p }[/math] of the fiber into the homotopy fiber is a homotopy equivalence. The mapping [math]\displaystyle{ i \colon F_p \to E }[/math] with [math]\displaystyle{ i (e, \gamma) = e }[/math], where [math]\displaystyle{ e \in E }[/math] and [math]\displaystyle{ \gamma \colon I \to B }[/math] is a path from [math]\displaystyle{ p(e) }[/math] to [math]\displaystyle{ b_0 }[/math] in the base space, is a fibration. Specifically it is the pullback fibration of the pathspace fibration [math]\displaystyle{ PB \to B }[/math]. This procedure can now be applied again to the fibration [math]\displaystyle{ i }[/math] and so on. This leads to a long sequence:
[math]\displaystyle{ \cdots \to F_j \to F_i \xrightarrow j F_p \xrightarrow i E \xrightarrow p B. }[/math]
The fiber of [math]\displaystyle{ i }[/math] over a point [math]\displaystyle{ e_0 \in p^{-1}(b_0) }[/math] consists of the pairs [math]\displaystyle{ (e_0, \gamma) }[/math] with closed paths [math]\displaystyle{ \gamma }[/math] and starting point [math]\displaystyle{ b_0 }[/math], i.e. the loop space [math]\displaystyle{ \Omega B }[/math]. The inclusion [math]\displaystyle{ \Omega B \to F }[/math] is a homotopy equivalence and iteration yields the sequence:
[math]\displaystyle{ \cdots \Omega^2B \to \Omega F \to \Omega E \to \Omega B \to F \to E \to B. }[/math]
Due to the duality of fibration and cofibration, there also exists a sequence of cofibrations. These two sequences are known as the Puppe sequences or the sequences of fibrations and cofibrations.[2]:407-409
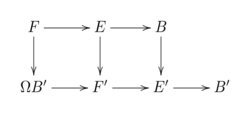
Principal fibration
A fibration [math]\displaystyle{ p \colon E \to B }[/math] with fiber [math]\displaystyle{ F }[/math] is called principal, if there exists a commutative diagram:
The bottom row is a sequence of fibrations and the vertical mappings are weak homotopy equivalences. Principal fibrations play an important role in Postnikov towers.[2]:412
Long exact sequence of homotopy groups
For a Serre fibration [math]\displaystyle{ p \colon E \to B }[/math] there exists a long exact sequence of homotopy groups. For base points [math]\displaystyle{ b_0 \in B }[/math] and [math]\displaystyle{ x_0 \in F = p^{-1}(b_0) }[/math] this is given by:
[math]\displaystyle{ \cdots \rightarrow \pi_n(F,x_0) \rightarrow \pi_n(E, x_0) \rightarrow \pi_n(B, b_0) \rightarrow \pi_{n - 1}(F, x_0) \rightarrow }[/math] [math]\displaystyle{ \cdots \rightarrow \pi_0(F, x_0) \rightarrow \pi_0(E, x_0). }[/math]
The homomorphisms [math]\displaystyle{ \pi_n(F, x_0) \rightarrow \pi_n(E, x_0) }[/math] and [math]\displaystyle{ \pi_n(E, x_0) \rightarrow \pi_n(B, b_0) }[/math] are the induced homomorphisms of the inclusion [math]\displaystyle{ i \colon F \hookrightarrow E }[/math] and the projection [math]\displaystyle{ p \colon E \rightarrow B. }[/math][2]:376
Hopf fibration
Hopf fibrations are a family of fiber bundles whose fiber, total space and base space are spheres:
[math]\displaystyle{ S^0 \hookrightarrow S^1 \rightarrow S^1, }[/math]
[math]\displaystyle{ S^1 \hookrightarrow S^3 \rightarrow S^2, }[/math]
[math]\displaystyle{ S^3 \hookrightarrow S^7 \rightarrow S^4, }[/math]
[math]\displaystyle{ S^7 \hookrightarrow S^{15} \rightarrow S^8. }[/math]
The long exact sequence of homotopy groups of the hopf fibration [math]\displaystyle{ S^1 \hookrightarrow S^3 \rightarrow S^2 }[/math] yields:
[math]\displaystyle{ \cdots \rightarrow \pi_n(S^1,x_0) \rightarrow \pi_n(S^3, x_0) \rightarrow \pi_n(S^2, b_0) \rightarrow \pi_{n - 1}(S^1, x_0) \rightarrow }[/math] [math]\displaystyle{ \cdots \rightarrow \pi_1(S^1, x_0) \rightarrow \pi_1(S^3, x_0) \rightarrow \pi_1(S^2, b_0). }[/math]
This sequence splits into short exact sequences, as the fiber [math]\displaystyle{ S^1 }[/math] in [math]\displaystyle{ S^3 }[/math] is contractible to a point:
[math]\displaystyle{ 0 \rightarrow \pi_i(S^3) \rightarrow \pi_i(S^2) \rightarrow \pi_{i-1}(S^1) \rightarrow 0. }[/math]
This short exact sequence splits because of the suspension homomorphism [math]\displaystyle{ \phi \colon \pi_{i - 1}(S^1) \to \pi_i(S^2) }[/math] and there are isomorphisms:
[math]\displaystyle{ \pi_i(S^2) \cong \pi_i(S^3) \oplus \pi_{i - 1}(S^1). }[/math]
The homotopy groups [math]\displaystyle{ \pi_{i - 1}(S^1) }[/math] are trivial for [math]\displaystyle{ i \geq 3, }[/math] so there exist isomorphisms between [math]\displaystyle{ \pi_i(S^2) }[/math] and [math]\displaystyle{ \pi_i(S^3) }[/math] for [math]\displaystyle{ i \geq 3. }[/math]
Analog the fibers [math]\displaystyle{ S^3 }[/math] in [math]\displaystyle{ S^7 }[/math] and [math]\displaystyle{ S^7 }[/math] in [math]\displaystyle{ S^{15} }[/math] are contractible to a point. Further the short exact sequences split and there are families of isomorphisms:[6]:111
[math]\displaystyle{ \pi_i(S^4) \cong \pi_i(S^7) \oplus \pi_{i - 1}(S^3) }[/math] and [math]\displaystyle{ \pi_i(S^8) \cong \pi_i(S^{15}) \oplus \pi_{i - 1}(S^7). }[/math]
Spectral sequence
Spectral sequences are important tools in algebraic topology for computing (co-)homology groups.
The Leray-Serre spectral sequence connects the (co-)homology of the total space and the fiber with the (co-)homology of the base space of a fibration. For a fibration [math]\displaystyle{ p \colon E \to B }[/math] with fiber [math]\displaystyle{ F, }[/math] where the base space is a path connected CW-complex, and an additive homology theory [math]\displaystyle{ G_* }[/math] there exists a spectral sequence:[7]:242
- [math]\displaystyle{ H_k (B; G_q(F)) \cong E^2_{k, q} \implies G_{k + q}(E). }[/math]
Fibrations do not yield long exact sequences in homology, as they do in homotopy. But under certain conditions, fibrations provide exact sequences in homology. For a fibration [math]\displaystyle{ p \colon E \to B }[/math] with fiber [math]\displaystyle{ F, }[/math] where base space and fiber are path connected, the fundamental group [math]\displaystyle{ \pi_1(B) }[/math] acts trivially on [math]\displaystyle{ H_*(F) }[/math] and in addition the conditions [math]\displaystyle{ H_p(B) = 0 }[/math] for [math]\displaystyle{ 0\lt p\lt m }[/math] and [math]\displaystyle{ H_q(F) = 0 }[/math] for [math]\displaystyle{ 0\lt q\lt n }[/math] hold, an exact sequence exists (also known under the name Serre exact sequence):
[math]\displaystyle{ H_{m+n-1}(F) \xrightarrow {i_*} H_{m+n-1}(E) \xrightarrow {f_*} H_{m+n-1} (B) \xrightarrow \tau H_{m+n-2} (F) \xrightarrow {i^*} \cdots \xrightarrow {f_*} H_1 (B) \to 0. }[/math][7]:250
This sequence can be used, for example, to prove Hurewicz's theorem or to compute the homology of loopspaces of the form [math]\displaystyle{ \Omega S^n: }[/math] [8]:162
[math]\displaystyle{ H_k (\Omega S^n) = \begin{cases} \Z & \exist q \in \Z \colon k = q (n-1)\\ 0 & else \end{cases}. }[/math]
For the special case of a fibration [math]\displaystyle{ p \colon E \to S^n }[/math] where the base space is a [math]\displaystyle{ n }[/math]-sphere with fiber [math]\displaystyle{ F, }[/math] there exist exact sequences (also called Wang sequences) for homology and cohomology:[1]:456
[math]\displaystyle{ \cdots \to H_q(F) \xrightarrow{i_*} H_q(E) \to H_{q-n}(F) \to H_{q-1}(F) \to \cdots }[/math] [math]\displaystyle{ \cdots \to H^q(E) \xrightarrow{i^*} H^q(F) \to H^{q-n+1}(F) \to H^{q+1}(E) \to \cdots }[/math]
Orientability
For a fibration [math]\displaystyle{ p \colon E \to B }[/math] with fiber [math]\displaystyle{ F }[/math] and a fixed commuative ring [math]\displaystyle{ R }[/math] with a unit, there exists a contravariant functor from the fundamental groupoid of [math]\displaystyle{ B }[/math] to the category of graded [math]\displaystyle{ R }[/math]-modules, which assigns to [math]\displaystyle{ b \in B }[/math] the module [math]\displaystyle{ H_*(F_b, R) }[/math] and to the path class [math]\displaystyle{ [\omega] }[/math] the homomorphism [math]\displaystyle{ h[\omega]_* \colon H_*(F_{\omega (0)}, R) \to H_*(F_{\omega (1)}, R), }[/math] where [math]\displaystyle{ h[\omega] }[/math] is a homotopy class in [math]\displaystyle{ [F_{\omega(0)}, F_{\omega (1)}]. }[/math]
A fibration is called orientable over [math]\displaystyle{ R }[/math] if for any closed path [math]\displaystyle{ \omega }[/math] in [math]\displaystyle{ B }[/math] the following holds: [math]\displaystyle{ h[\omega]_* = 1. }[/math][1]:476
Euler characteristic
For an orientable fibration [math]\displaystyle{ p \colon E \to B }[/math] over the field [math]\displaystyle{ \mathbb{K} }[/math] with fiber [math]\displaystyle{ F }[/math] and path connected base space, the Euler characteristic of the total space is given by:
[math]\displaystyle{ \chi(E) = \chi(B)\chi(F). }[/math]
Here the Euler characteristics of the base space and the fiber are defined over the field [math]\displaystyle{ \mathbb{K} }[/math].[1]:481
See also
References
- ↑ 1.0 1.1 1.2 1.3 1.4 Spanier, Edwin H. (1966). Algebraic Topology. McGraw-Hill Book Company. ISBN 978-0-387-90646-1.
- ↑ 2.00 2.01 2.02 2.03 2.04 2.05 2.06 2.07 2.08 2.09 2.10 2.11 2.12 2.13 Hatcher, Allen (2001). Algebraic Topology. NY: Cambridge University Press. ISBN 0-521-79160-X.
- ↑ Dold, Albrecht; Thom, René (1958). "Quasifaserungen und Unendliche Symmetrische Produkte". Annals of Mathematics 67 (2): 239–281. doi:10.2307/1970005.
- ↑ 4.0 4.1 Laures, Gerd; Szymik, Markus (2014) (in German). Grundkurs Topologie (2nd ed.). Springer Spektrum. doi:10.1007/978-3-662-45953-9. ISBN 978-3-662-45952-2.
- ↑ May, J.P. (1999). A Concise Course in Algebraic Topology. University of Chicago Press. ISBN 0-226-51182-0. OCLC 41266205. http://www.math.uchicago.edu/~may/CONCISE/ConciseRevised.pdf.
- ↑ Steenrod, Norman (1951). The Topology of Fibre Bundles. Princeton University Press. ISBN 0-691-08055-0.
- ↑ 7.0 7.1 Davis, James F.; Kirk, Paul (1991). Lecture Notes in Algebraic Topology. Department of Mathematics, Indiana University. https://jfdmath.sitehost.iu.edu/teaching/m623/book.pdf.
- ↑ Cohen, Ralph L. (1998). The Topology of Fiber Bundles Lecture Notes. Stanford University. https://math.stanford.edu/~ralph/fiber.pdf.
 |