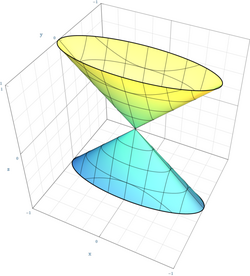
Conical surface
In geometry, a conical surface is a three-dimensional surface formed from the union of lines that pass through a fixed point and a space curve.
Definitions
A (general) conical surface is the unbounded surface formed by the union of all the straight lines that pass through a fixed point — the apex or vertex — and any point of some fixed space curve — the directrix — that does not contain the apex. Each of those lines is called a generatrix of the surface. The directrix is often taken as a plane curve, in a plane not containing the apex, but this is not a requirement.[1]
In general, a conical surface consists of two congruent unbounded halves joined by the apex. Each half is called a nappe, and is the union of all the rays that start at the apex and pass through a point of some fixed space curve.[2] Sometimes the term "conical surface" is used to mean just one nappe.[3]
Special cases
If the directrix is a circle [math]\displaystyle{ C }[/math], and the apex is located on the circle's axis (the line that contains the center of [math]\displaystyle{ C }[/math] and is perpendicular to its plane), one obtains the right circular conical surface or double cone.[2] More generally, when the directrix [math]\displaystyle{ C }[/math] is an ellipse, or any conic section, and the apex is an arbitrary point not on the plane of [math]\displaystyle{ C }[/math], one obtains an elliptic cone[4] (also called a conical quadric or quadratic cone),[5] which is a special case of a quadric surface.[4][5]
Equations
A conical surface [math]\displaystyle{ S }[/math] can be described parametrically as
- [math]\displaystyle{ S(t,u) = v + u q(t) }[/math],
where [math]\displaystyle{ v }[/math] is the apex and [math]\displaystyle{ q }[/math] is the directrix.[6]
Related surface
Conical surfaces are ruled surfaces, surfaces that have a straight line through each of their points.[7] Patches of conical surfaces that avoid the apex are special cases of developable surfaces, surfaces that can be unfolded to a flat plane without stretching. When the directrix has the property that the angle it subtends from the apex is exactly [math]\displaystyle{ 2\pi }[/math], then each nappe of the conical surface, including the apex, is a developable surface.[8]
A cylindrical surface can be viewed as a limiting case of a conical surface whose apex is moved off to infinity in a particular direction. Indeed, in projective geometry a cylindrical surface is just a special case of a conical surface.[9]
See also
References
- ↑ Adler, Alphonse A. (1912), "1003. Conical surface", The Theory of Engineering Drawing, D. Van Nostrand, p. 166, https://archive.org/details/cu31924003943481/page/n185
- ↑ 2.0 2.1 Wells, Webster; Hart, Walter Wilson (1927), Modern Solid Geometry, Graded Course, Books 6-9, D. C. Heath, pp. 400–401, https://books.google.com/books?id=vXENAQAAIAAJ&pg=PA400
- ↑ Shutts, George C. (1913), "640. Conical surface", Solid Geometry, Atkinson, Mentzer, p. 410, https://books.google.com/books?id=9zAAAAAAYAAJ&pg=PA410
- ↑ 4.0 4.1 Young, J. R. (1838), Analytical Geometry, J. Souter, p. 227, https://archive.org/details/analyticalgeome00youngoog/page/n243
- ↑ 5.0 5.1 Odehnal, Boris; Stachel, Hellmuth; Glaeser, Georg (2020), "Linear algebraic approach to quadrics", The Universe of Quadrics, Springer, pp. 91–118, doi:10.1007/978-3-662-61053-4_3, ISBN 9783662610534
- ↑ Gray, Alfred (1997), "19.2 Flat ruled surfaces", Modern Differential Geometry of Curves and Surfaces with Mathematica (2nd ed.), CRC Press, pp. 439–441, ISBN 9780849371646, https://books.google.com/books?id=-LRumtTimYgC&pg=PA439
- ↑ Mathematical Society of Japan (1993), Ito, Kiyosi, ed., Encyclopedic Dictionary of Mathematics, Vol. I: A–N (2nd ed.), MIT Press, p. 419, https://books.google.com/books?id=WHjO9K6xEm4C&pg=PA419
- ↑ Audoly, Basile; Pomeau, Yves (2010), Elasticity and Geometry: From Hair Curls to the Non-linear Response of Shells, Oxford University Press, pp. 326–327, ISBN 9780198506256, https://books.google.com/books?id=FMQRDAAAQBAJ&pg=PA326
- ↑ Giesecke, F. E.; Mitchell, A. (1916), Descriptive Geometry, Von Boeckmann–Jones Company, p. 66, https://books.google.com/books?id=sCc7AQAAMAAJ&pg=PA66
 |