Binary entropy function
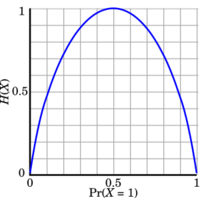
In information theory, the binary entropy function, denoted [math]\displaystyle{ \operatorname H(p) }[/math] or [math]\displaystyle{ \operatorname H_\text{b}(p) }[/math], is defined as the entropy of a Bernoulli process with probability [math]\displaystyle{ p }[/math] of one of two values. It is a special case of [math]\displaystyle{ \Eta(X) }[/math], the entropy function. Mathematically, the Bernoulli trial is modelled as a random variable [math]\displaystyle{ X }[/math] that can take on only two values: 0 and 1, which are mutually exclusive and exhaustive.
If [math]\displaystyle{ \operatorname{Pr}(X=1) = p }[/math], then [math]\displaystyle{ \operatorname{Pr}(X=0) = 1-p }[/math] and the entropy of [math]\displaystyle{ X }[/math] (in shannons) is given by
- [math]\displaystyle{ \operatorname H(X) = \operatorname H_\text{b}(p) = -p \log_2 p - (1 - p) \log_2 (1 - p) }[/math],
where [math]\displaystyle{ 0 \log_2 0 }[/math] is taken to be 0. The logarithms in this formula are usually taken (as shown in the graph) to the base 2. See binary logarithm.
When [math]\displaystyle{ p=\tfrac 1 2 }[/math], the binary entropy function attains its maximum value. This is the case of an unbiased coin flip.
[math]\displaystyle{ \operatorname H(p) }[/math] is distinguished from the entropy function [math]\displaystyle{ \Eta(X) }[/math] in that the former takes a single real number as a parameter whereas the latter takes a distribution or random variable as a parameter. Sometimes the binary entropy function is also written as [math]\displaystyle{ \operatorname H_2(p) }[/math]. However, it is different from and should not be confused with the Rényi entropy, which is denoted as [math]\displaystyle{ \Eta_2(X) }[/math].
Explanation
In terms of information theory, entropy is considered to be a measure of the uncertainty in a message. To put it intuitively, suppose [math]\displaystyle{ p=0 }[/math]. At this probability, the event is certain never to occur, and so there is no uncertainty at all, leading to an entropy of 0. If [math]\displaystyle{ p=1 }[/math], the result is again certain, so the entropy is 0 here as well. When [math]\displaystyle{ p=1/2 }[/math], the uncertainty is at a maximum; if one were to place a fair bet on the outcome in this case, there is no advantage to be gained with prior knowledge of the probabilities. In this case, the entropy is maximum at a value of 1 bit. Intermediate values fall between these cases; for instance, if [math]\displaystyle{ p=1/4 }[/math], there is still a measure of uncertainty on the outcome, but one can still predict the outcome correctly more often than not, so the uncertainty measure, or entropy, is less than 1 full bit.
Derivative
The derivative of the binary entropy function may be expressed as the negative of the logit function:
- [math]\displaystyle{ {d \over dp} \operatorname H_\text{b}(p) = - \operatorname{logit}_2(p) = -\log_2\left( \frac{p}{1-p} \right) }[/math].
Taylor series
The Taylor series of the binary entropy function in a neighborhood of 1/2 is
- [math]\displaystyle{ \operatorname H_\text{b}(p) = 1 - \frac{1}{2\ln 2} \sum^{\infin}_{n=1} \frac{(1-2p)^{2n}}{n(2n-1)} }[/math]
for [math]\displaystyle{ 0\le p\le 1 }[/math].
Bounds
The following bounds hold for [math]\displaystyle{ 0 \lt p \lt 1 }[/math]:[1]
- [math]\displaystyle{ \ln(2) \cdot \log_2(p) \cdot \log_2(1-p) \leq H_\text{b}(p) \leq \log_2(p) \cdot \log_2(1-p) }[/math]
and
- [math]\displaystyle{ 4p(1-p) \leq H_\text{b}(p) \leq (4p(1-p))^{(1/\ln 4)} }[/math]
where [math]\displaystyle{ \ln }[/math] denotes natural logarithm.
See also
- Metric entropy
- Information theory
- Information entropy
- Quantities of information
References
- ↑ "Bounds for entropy and divergence for distributions over a two-element set.". JIPAM. Journal of Inequalities in Pure & Applied Mathematics 2 (2): Paper No. 25, 13 p.-Paper No. 25, 13 p. 2001. http://eudml.org/doc/122035.
Further reading
- MacKay, David J. C. Information Theory, Inference, and Learning Algorithms Cambridge: Cambridge University Press, 2003. ISBN:0-521-64298-1
zh-yue:二元熵函數
 |

