Biology:Multiplicity of infection
In microbiology, the multiplicity of infection or MOI is the ratio of agents (e.g. phage or more generally virus, bacteria) to infection targets (e.g. cell). For example, when referring to a group of cells inoculated with virus particles, the MOI is the ratio of the number of virus particles to the number of target cells present in a defined space.[1]
Interpretation
The actual number of viruses or bacteria that will enter any given cell is a stochastic process: some cells may absorb more than one infectious agent, while others may not absorb any. Before determining the multiplicity of infection, it's absolutely necessary to have a well-isolated agent, as crude agents may not produce reliable and reproducible results. The probability that a cell will absorb [math]\displaystyle{ n }[/math] virus particles or bacteria when inoculated with an MOI of [math]\displaystyle{ m }[/math] can be calculated for a given population using a Poisson distribution. This application of Poisson's distribution was applied and described by Ellis and Delbrück.[2]
- [math]\displaystyle{ P(n) = \frac{m^n \cdot e^{-m}}{n!} }[/math]
where [math]\displaystyle{ m }[/math] is the multiplicity of infection or MOI, [math]\displaystyle{ n }[/math] is the number of infectious agents that enter the infection target, and [math]\displaystyle{ P(n) }[/math] is the probability that an infection target (a cell) will get infected by [math]\displaystyle{ n }[/math] infectious agents.
In fact, the infectivity of the virus or bacteria in question will alter this relationship. One way around this is to use a functional definition of infectious particles rather than a strict count, such as a plaque forming unit for viruses.[3]
For example, when an MOI of 1 (1 infectious viral particle per cell) is used to infect a population of cells, the probability that a cell will not get infected is [math]\displaystyle{ P(0) = 36.79\% }[/math], and the probability that it be infected by a single particle is [math]\displaystyle{ P(1) = 36.79\% }[/math], by two particles is [math]\displaystyle{ P(2)=18.39\% }[/math], by three particles is [math]\displaystyle{ P(3) = 6.13\% }[/math], and so on.
The average percentage of cells that will become infected as a result of inoculation with a given MOI can be obtained by realizing that it is simply [math]\displaystyle{ P(n\gt 0) = 1 - P(0) }[/math]. Hence, the average fraction of cells that will become infected following an inoculation with an MOI of [math]\displaystyle{ m }[/math] is given by:
- [math]\displaystyle{ P(n\gt 0) = 1 - P(n=0) = 1 - \frac{m^0 \cdot e^{-m}}{0!} = 1 - e^{-m} }[/math]
which is approximately equal to [math]\displaystyle{ m }[/math] for small values of [math]\displaystyle{ m \ll 1 }[/math].
Examples
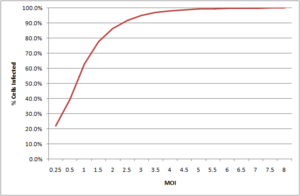
As the MOI increases, the percentages of cells infected with at least one viral particle also increases.[4]
| MOI | % Infected |
|---|---|
| 1.0 | 63.2% |
| 2.0 | 86.5% |
| 3.0 | 95.0% |
| 4.0 | 98.2% |
| 5.0 | 99.3% |
| 6.0 | 99.8% |
| 7.0 | 99.9% |
| 8.0 | ~100.0% |
See also
References
- ↑ Abedon, S. T.; Bartom, E. (2013-01-01), Maloy, Stanley; Hughes, Kelly, eds. (in en), Multiplicity of Infection, San Diego: Academic Press, pp. 509–510, ISBN 978-0-08-096156-9, https://www.sciencedirect.com/science/article/pii/B978012374984000989X, retrieved 2022-03-09
- ↑ Ellis, Emory; Delbruck, Max (Jan 20, 1939). "The Growth of Bacteriophage". The Journal of General Physiology 22 (3): 365–384. doi:10.1085/jgp.22.3.365. PMID 19873108.
- ↑ "Plaque forming unit". https://www.sciencedirect.com/topics/immunology-and-microbiology/plaque-forming-unit.
- ↑ Fields virology: Part 1. Philadelphia: Wolters Kluwer Health/Lippincott Williams & Wilkins. 2007. ISBN 9780781760607. OCLC 71812790.
 |