DMelt:ExternalGuides/Medusa
Most essential information on Medusa
Here we repost some of the most useful information on Medusa application. More information can be found in [1]
Clustering Algorithms
Predefined Clustering
Users can run their own clustering algorithm independently and plug the results directly to Medusa application for visualization. Nodes that belong to the same layer will come together around a circle whereas each cluster will get assigned a different color.
Affinity Propagation
Affinity Propagation algorithms is a machine learning based algorithm which can be used in interdisciplinary fields to cluster data. This algorithm is fast and efficient and takes as input measures of similarity between pairs of data points and simultaneously considers all data points as potential exemplars. Real-valued messages are exchanged between data points until a high-quality set of exemplars and corresponding clusters gradually emerges. The user does not have to define the number of clusters since they are automatically calculated. This algorithm can also be used in biological cases. In the original paper the authors show how Affinity Propagation can efficiently identify segments of DNA that reflect the expression properties of genes.
Complexity: O((N^2)log(N)) where N is the number of nodes
Spectral Clustering
Spectral clustering is a supervised clustering method where the user needs to define the number of cluster like in k-Means. Spectral methods allow one to study global properties of a dataset by making only pairwise similarity measurements between data points. Spectral clustering considers partitioning a weighted undirected graph G into a set of discrete clusters. Each node in the graph corresponds to a protein sequence and the weight on each edge corresponds to the similarity between the two protein sequences it connects. Ideally, we are looking for areas in the graph, the clusters, in which the nodes are connected with highly-similar edges; and at the same time the connections between such areas should be weak, constituted by edges with low similarity. Spectral algorithms was extensively tested and compared with other local methods on several subsets of the Structural Classification of Proteins database, a gold standard for protein structure classification. We consistently observed that, the number of clusters that we obtain for a given set of proteins is close to the number of superfamilies in that set; there are fewer singletons; and the method correctly groups most remote homologs. Its biological applicability can be explained extensively in the relevant article.
Complexity: The complexity of this algorithm is not defined yet but it is definitely slower that the rest algorithms described here.
PARAMETERS: User needs to provide a parameter which shows the number of clusters
k-Means
k-Means (MacQueen, 1967) is an algorithm to cluster data. It is necessary for the user to define the number of clusters (k) manually. It is not often used in biological cases but it is a very well known and widely used algorithms that can be used in interdisciplinary fields. k-Means accepts as an input a full all-against-all distance matrix and has a running time complexity of O(nlk) were n is the number of nodes, l is the number of loops and k the number of clusters.The procedure follows a simple and easy way to classify a given data set through a certain number of clusters (assume k clusters) fixed a priori. The main idea is to define k centroids, one for each cluster. These centroids shoud be placed in a cunning way because of different location causes different result. So, the better choice is to place them as much as possible far away from each other. The next step is to take each point belonging to a given data set and associate it to the nearest centroid. When no point is pending, the first step is completed and an early groupage is done. At this point we need to re-calculate k new centroids as barycenters of the clusters resulting from the previous step. After we have these k new centroids, a new binding has to be done between the same data set points and the nearest new centroid. A loop has been generated. As a result of this loop we may notice that the k centroids change their location step by step until no more changes are done. In other words centroids do not move any more. It is a suitable algorithms when all of the relationships among all of the data points are known.
Complexity: O(nlk) where n is the number of nodes, k is the number of user predefined clusters and l the number of loops where the algorithm diverges.
Layout Algorithms
Random
Nodes are placed randomly on the plane. This layout is intuitive for smaller networks and not easy to analyze for bigger networks. An example is shown in the figure. It can be e very intuitive layout when nodes edges of specific nodes are isolated. It can get very confusing and difficult to follow when the whole network with its full complexity is visualized.
Grid
Nodes are placed on a grid. This layout is useful for networks with specific structure. Visually this layout is very nice when specific edges of specific nodes are shown.
Circular
Nodes are placed around a circle. This layout is intuitive for smaller networks and not easy to analyze for bigger networks.
Fruchterman-Reingold
It is Force-based or force-directed algorithm to draw graphs in an aesthetically pleasing way. Its purpose is to position the nodes of a graph in 2D so that all the edges are of more or less equal length and there are as few crossing edges as possible. The strength of this algorithms is that with such a layout, patterns such as highly connected regions or hubs can immediately get observed.
Relax- cooling
This layout as an interactive module so to follow how the dynamics of the network changes interactively. Start/Stop cooling options give to the user the opportunity to stop the layout when he likes. it is a great layout to make highly connected nodes visible. By draging one node the whole network changes. Nodes can be pulled or fixed (see below) to enhance the visualisation. Cooling This option, when toggled on, causes the linear spring to cool down over time. This removes any potential "jittering" in large networks due to integer rounding issues. Clicking a node in this mode will raise the temperature back up to the initial value before decreasing again.
Distance geometry
This layout can be applied on weighted graphs. Te purpose of this algorithm is to bring closer nodes that are stronger connected and place nodes that are weakly connected further away. Suppose that we have a case study of sequence alignment between proteins or expression profiles of genes. The genes that have similar expression profiles or the proteins that have higher sequence similarity will come together.
Hierarchical
This layout places nodes in a hierarchy according to the edge weights. It is a very efficient layout for sparse graphs with tree-like hierarchies such as gene ontologies. It is the same layout used in GraphViz.
Parallel axes
This layout was inspired from multi-layered graphs. Data that belong onto different layers are separated and linked together. Nodes can get connected within the same layer or among layers. It is a great layout algorithm to visualize time series data (each layer to represent a different tie point.)
File format
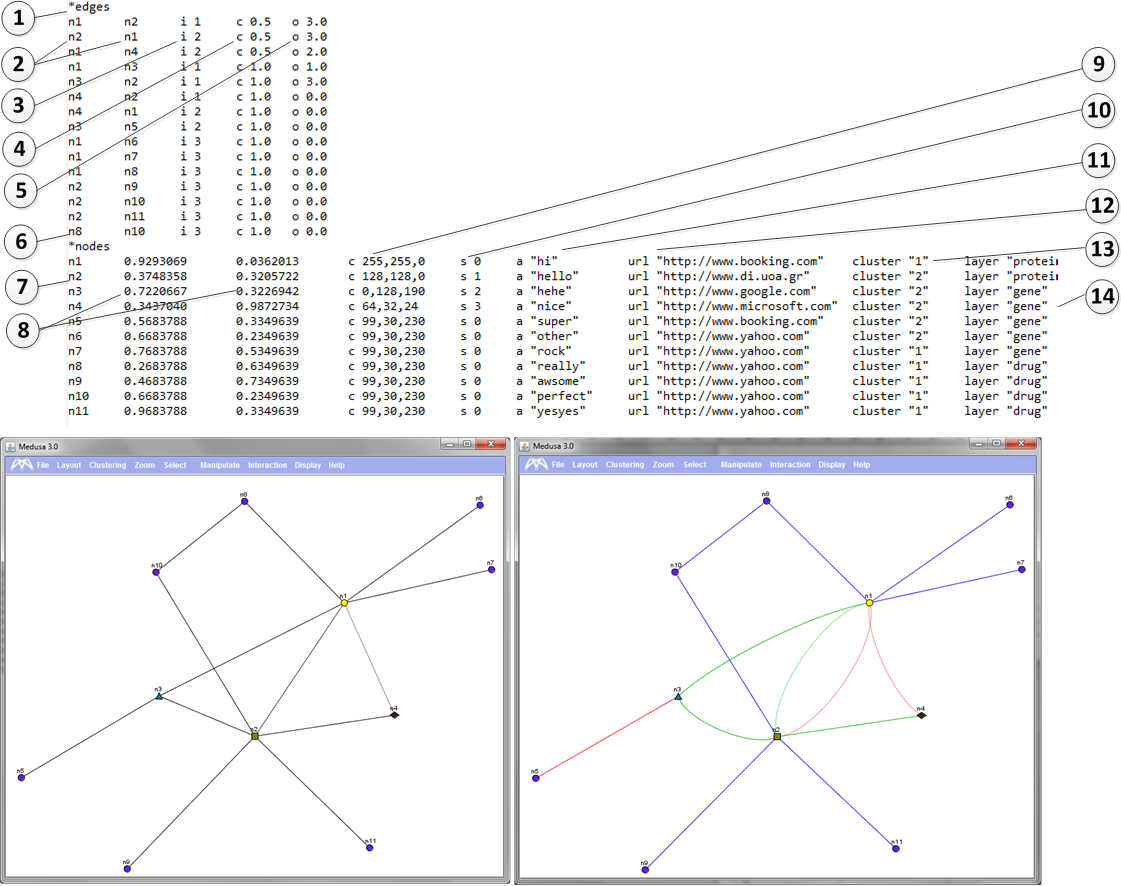 1) *edges
This tag indicates that the section that will follow contains information about the edges. The nodes of th edges should be declared in the node section. See below.
1) *edges
This tag indicates that the section that will follow contains information about the edges. The nodes of th edges should be declared in the node section. See below.
2) n2 n1 Nodes that are connected (in this case n2 and n1) should be tab seperated.
3) i parameter
Parameter i is followed by a single space and then by a value. The values can range from 1-10. This parameter indicates the type of the interaction between two nodes.
For example the right image shows that nodes n1 and n2 are connected with 2 different types of connections. (See line 2 and 3 of the file)
Before this column a tab is required.
4) c parameter Parameter c is followed by a single space and then by a value. The values can range from 0-1. This parameter indicates the strength of the connection between two nodes. For example the right image shows that nodes n1 and n2 are NOT so strongly connected and this is why the color of the nodes appears weaker. Before this column a tab is required.
5) o parameter Parameter i is followed by a single space and then by a value. The values can be >0. This parameter indicates how much curvy the lines between two nodes will be. For example the right image shows that nodes n1 and n2 have o-value 3. If o parameter equals to 0 ten the line appears as straight. Before this column a tab is required.
6) *nodes - This tag indicates that the section that will follow contains information about the nodes.
7) n2 - The line starts with the node name which is then followed by a tab.
8) X,Y coordinates - Float values are given in two tab delimited columns. these indicate the X and the Y coordinates of the node. In this case for example node n3 has coordinates (0.7220667, 0.3226942). Before the X and the Y column a tab is required.
9) c parameter. - Parameter c is followed by a single space and then by a triple comma separated value. Each values can range between (0-255) . This parameter indicates the color of the node in RGB format. For example, node n1 has color (255,255,0). Before this column a tab is required.
10) s parameter. - Parameter s is followed by a single space and then by an integer value. Values can range between (0-3) . This parameter indicates the shape of the node. (0=circle, 1= rectangle, 2=triangle, 3=diamond) An example is shown on the right image. (See nodes n1, n2, n3, n4) Before this column a tab is required.
11) a parameter. - Parameter a is followed by a single space and then by a string between " " characters. This parameter indicates the annotations of the node. Before this column a tab is required.
12) url parameter. - Parameter url is followed by a single space and then by string between " " characters. This parameter indicates the URL of the node. This way predefined link-outs are allowed. It is not an optional parameter. Before this column a tab is required.
13) cluster parameter. - Parameter cluster is followed by a single space and then by a integer between " " characters. The range of the integer can be >0. This parameter indicates the pre-definded cluster that a node belongs to. Pre-defined cluster ca be calculated by external applications not hosted in Medusa. It is not an optional parameter. Before this column a tab is required.
14) layer parameter. -
Parameter layer is followed by a single space and then by string between " " characters.
This parameter indicates the layer of the node.
It is mainly used to visualize multi-layered graphs or time series data.
It is not an optional parameter.
Before this column a tab is required.
